Геометрични приложения на линия интеграли
Площта на региона ограничена от затворена крива;
Обемът на тялото, образуван от въртенето на затворена крива около ос.
Нека \ (С \) е гладка, по части непрекъсната крива, която е описана от вектор \ (\ mathbf \ наляво (т \ полето), \, \ а \ ле т \ ле \ бета. \) На дължината на кривата се изразява в следния ред неразделна \ [> = >>> \ наляво (т \ дясно)> \ полето | DT >> = >>> \ дясно)> ^ 2> + >>> \ дясно)> ^ 2> + >>> \ дясно) > ^ 2 >> DT>,> \], където \ (\ голям \ Frac >>> \ normalsize \) - производно и \ (х \ наляво (т \ полето), у \ наляво (т \ полето), Z \ наляво (т \ дясно) \) - компоненти вектор функция \ (\ mathbf \ наляво (т \ дясно) \).
Ако крива \ (С \) се определя в една равнина, а след това му дължина е дадено от \ [> = >>> \ наляво (т \ дясно)> \ полето | DT >> = >>> \ дясно)> ^ 2> +> >> \ дясно)> ^ 2 >> DT>.> \] Ако крива \ (C \) е графика изрично предварително определена, непрекъсната и диференцируема функция \ (у = F \ наляво (х \ дясно) \) в равнината \ (окси \) след това продължителността на такава крива се изчислява по формула \ [L = \ Int \ limits_a ^ б >>> \ дясно)> ^ 2 >> DX>. \] И накрая, ако крива \ (с \) е даден в полярен координира от уравнение \ (R = R \ наляво (\ тета \ полето), \, \ а \ ле \ тета \ ле \ р \) функция \ и (г \ ляво (\ тета \ дясно) \) е непрекъсната и диференцируема в интервал \ на (\ наляво [\ полето] \) след това дължината на крива се определя от експресия \ [L = \ Int \ limits_ \ алфа ^ \ бета >>> \ дясно)> ^ 2> +> г \ тета>. \]
Площта на района, ограничен от затворената крива
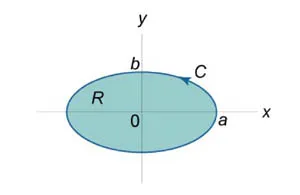
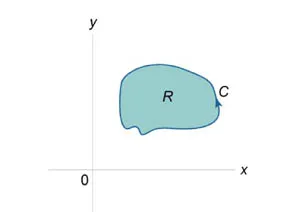
Нека \ (С \) е гладка, по части непрекъсната затворена крива дефинирани в равнина \ (окси \) (Фигура \ (1 \)). След областта на област \ (R, \) Limited на кривата, определена от формула \ [= -. \ Съвместният \ limits_C> = \ Int \ limits_C> \] Предполага се, че тук байпас крива \ на (С \) е обратна на часовниковата стрелка.
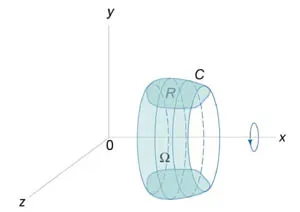
Обемът на тялото, образуван от въртенето на затворена крива по отношение на оста Ox
Да приемем, че площ \ (R \), разположени в горната половина \ (у \ GE 0 \) и ограничен от гладка, по части непрекъсната и затворена крива \ (С \), който байпаса на часовниковата стрелка. В резултат на това въртене област \ на (R \) около \ ос (Ox \) се образува тяло \ (\ Omega \) (Фигура \ (2 \)). Обемът на организма се определя от формули \ [DX >> = <- 2\pi \oint\limits_C> = <- \frac\oint\limits_C dx> .> \]
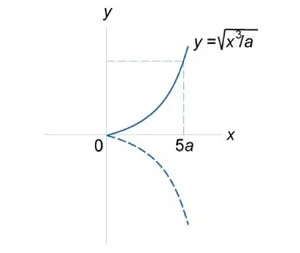
Виж дължината на кривата \ (а = \) дава \ (0 \ ле х \ ле 5а, \, г \ GE 0. \)
Намери дължината на кривата на пространство определено параметрично като \ (\ mathbf \ наляво (т \ дясно) = \ наляво (2> \ полето), \), където \ (0 \ ле т \ ле 1. \)
Виж циклоида дължина дефинирани параметрично вектор \ (\ mathbf \ наляво (т \ дясно) = \ наляво (\ полето), а \ наляво (\ дясно)> \ дясно) \) в интервал \ на (0 \ ле т \ Le 2 \ пи \) (Фигура \ (5 \)).
Виж областта на региона ограничена от хипербола \ (у = \ голям \ Frac \ normalsize \) ос \ (Ox \) и вертикални линии \ (х = 1, \) \ (х = 2 \) (Фигура \ (7 \) ).
Изчисляваме района с помощта на линия неразделна. \ [> = <- \int\limits_ - \int\limits_ - \int\limits_ - \int\limits_ .> \] Намираме поотделно всеки един от интегралите. \ [- \ Int \ limits_ = - \ Int \ limits_1 ^ 2 = 0, \] \ [- \ Int \ limits_ = - \ Int \ limits_0 ^ 0 = 0, \] \ [= - \ Int \ limits_2 ^ 1 >>> = \ дясно)> \ дясна | _2 ^ 1> = <- \ln 1 + \ln 2 = \ln 2,> \] \ [- \ Int \ limits_ = - \ Int \ limits_0 ^ 0 = 0 \] Следователно, предварително определена зона е зона \ [S = \ LN 2. \]
Виж областта на област, ограничена от елипса посочено параметрично като \ (х = а \ защото т, \; у = б \ грях т \ 0 \ ле т \ ле 2 \ пи \) (Фигура \ (8 \)) ,