Функция у TGX, Y ctgx, техните свойства и графики

§ 15. функции у = TGX, у = ctgx, техните свойства и графици

Имайте предвид свойствата на функцията у = х TG, и особено тези, които помагат да се направи представяне за графиката на (по-голямата част от тези имоти са всъщност познат ни от § 5). Когато такова представяне върви добре, ще започнем да изготвите график, както обикновено, по точки.

Property 1. Домейнът на функция у = х TG - набор от реални числа, с изключение на номерата на формата

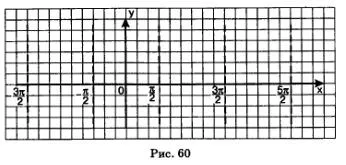
Този имот означава, че функцията за графика не е на мястото, не е собственост на директна точка, принадлежащ на една права линия няма смисъл, принадлежащ на една права линия, и т.н. Тези линии, държани от пунктирани линии на фиг. 60.

Първото представяне на графиката, получена чрез: тя се състои от безкраен брой клонове (в обхвата от
Имота 2. у = TG х периодична функция с основен период п.
Това следва от уравнението, получена в двойна § 5.
Така че, ако ние конструираме графика клон в групата на тогава ще трябва да се движат на клона построен по оста х в дясно и в ляво от п, 2п, Sn и т.н. Така Teck получи втора снимка на графиката.

3. имущество = TG х е нечетен функция. От това следва, от това, което е доказано в съотношение § 5 график странно функция симетрична спрямо. Така че можем да се процедира, както следва: за изграждане на част от точките парцел на интервал от и след това да се възползвате от тази симетрия.

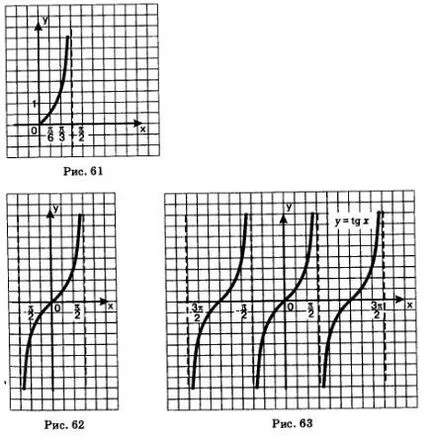
Нека се построи графиката на интервал. Изберете контролен пункт:

Имайте предвид следните точки на координатната равнина и да се прави гладка крива чрез тях (фиг. 61). Добави линия крива конструиран симетрично по отношение на произхода (фиг. 62). Използването на интервали трябва да изпълни графика до края (фиг. 63).

Графиката на у = TG х tangensoidoy наречен. Тази част, която е показана на Фиг. 62, обикновено се нарича като основен клон tangensoidy.

Имайте предвид, че произход tangensoidy главен клон, както ако под ъгъл от 45 °. Защо това е така, ще научите в глава 4.

Имоти 4. Функцията увеличава интервала в по-общ смисъл - функцията се увеличава на всеки интервал от формата
Имота 5. функция у = TG къна Ограниченият или отгоре или отдолу.

6. функция имот в х = TG не най-голямата или най-малката стойност Sheha.
Имота 7. функция у = TG х е непрекъсната върху интервала в по-общ начин - е непрекъснато на всеки интервал на формата
Когато стойността на функцията е прекъсната. Всеки ред е един вид вертикални asimptotoi графика на функцията.

Така, а това означава увеличение на у функция = TG х от избрания интервал.
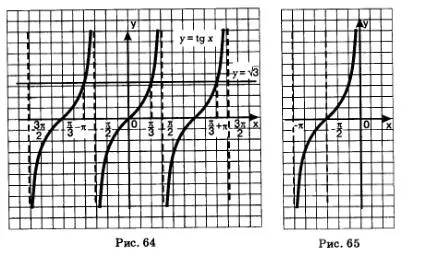
Пример 1. решаване на уравнение х = Tg
Решение. Разположен в една графика координатна система на функции у = TG х - и у = tangensoidu - линия, успоредна на х-оста. Те имат безкрайно много точки на пресичане (фиг. 64), а абсцисната на точките се различават един от друг на компютъра. В основните отрасли на абсцисата на съответната точка е (ние използвахме известно цифров равенство - е един корен на уравнението и всички разтвори са описани с формулата
отговори на:

Пример 2. функция Парцел
Решение. За да започнете, нека да се справят с главния клон tangensoidy.
1) се пристъпи към спомагателна координатна система с произхода на мястото проведе фиг. 65 пунктирана линия).
2) функция "Равенство" в TG = х * нова координатна система - това е функция график. по-скоро, основната клон на желания графиката (виж фигура 65 -. твърдата кривата).
3) За получаване на графиката на дисплея на функция достатъчно построен клон симетрично спрямо оста х (фиг. 66).
4) Знаейки един клон, може да се изгради цялата графика (фиг. 67).

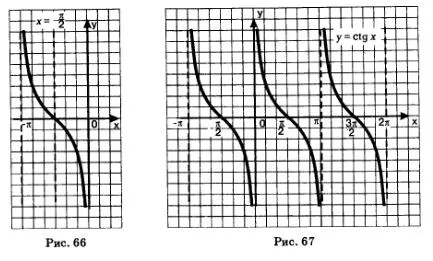
В действителност, на фиг. 67 построена от графиката на у = stgh. Защо? Тъй идентичност (формула намаляване) на
Графиката на функция у = х CTG като графиката на функция Y = TG х, наречен tangensoidoy. Основната клон на графиката на у = функция х CTG обикновено се нарича клон затворено в групата от х = 0 до х = к.
Пример 3: решаване на уравнение CTG х = 1.

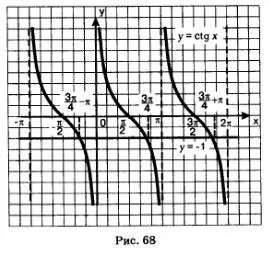
Решение. Ние конструкт в координатна система графики функция у = а х CTG - tangensoidu и у = 1 - линия, паралелна на оста х. Те имат безкраен брой точки на пресичане (фиг. 68), а абсцисната на тези точки са различни един от друг в Jap. В основните отрасли на абсцисата, съответстващ на точка е (ние използвахме добре познати равенство: и всички разтвори на даденото уравнение могат да бъдат покрити с формула
отговори на:

AG Mordkovich Алгебра 10 клас

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.