Експерименти с бутилка Klein, публикация в списание "млад учен"

Тази статия представя опита с Klein бутилка. Породени проблема и решен експериментално, прогнозиране експерименти с режещо модел на бутилката Клайн. неговите свойства са били идентифицирани.

Думи: Klein бутилка, на Мьобиус ивица, триизмерното пространство, топологичното повърхността.

Abstract.The статия представя серия от експерименти с бутилката Клайн. Решава проблема за прогнозиране на резултатите от експеримента с рязане на бутилката Клайн. Ние също така се идентифицират неговите свойства.

Ключови думи: бутилката Klein, на ивица Мьобиус, триизмерно пространство, топологична повърхност.

Klein бутилка е описан от германски учен от Klein през 1882.

С бутилка Klein са въведени във висшите учебни заведения в хода на геометрията. Този модел е интересно, защото неговите качества не могат да се видят, без провеждане на експерименти, защото тя не може да съществува в нашето триизмерно пространство. Моделите, които виждаме в магазините, като сувенир са отдалечени на шишето Клайн. Интересна възможност за определяне на свойствата на бутилката Klein чрез експерименти.

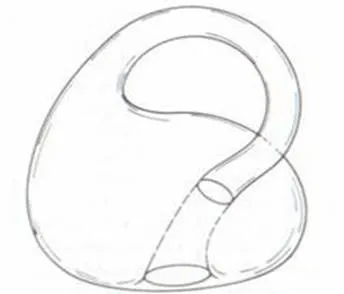
Фиг.1. Клайн бутилка

Klein бутилка - това е определен неориентируема повърхност [1, стр. 352]. Това се дължи отчасти на Мьобиус ивица на (правоъгълна лента, получена чрез залепване противоположните страни завърта на 180 градуса [3]) и проективна равнина.

Осъществяване на бутилка Klein

Фиг. 2. Производство на бутилката Klein

Fold наполовина квадрата и се свързва към страните, определени от прекъснатата линия на фигура 1 а). Направи прорез върху страната, обърната към вас половина на квадрат, перпендикулярна на лепени страна на фигура 1 Ь). Между горния ръб и навреме тръба трябва да бъде на разстояние, равно на една четвърт от квадрата. Огъване модела наполовина по линия А-А плъзгане долния край на тръбата през отвора, лепило заедно горната и долната тръба база в съответствие със стрелките на фигура 1).

Виждаме, че лепилото е трудно бутилка Клайн. От прозрачен материал, този модел ще бъде по-ясно. Освен провежда серия от експерименти с бутилка Klein описани в таблица 1.

Първоначално предположението, ще бъде направено, какъв ще бъде резултатът, а след това се проверява предположения, направени от нас.

Рязане на бутилката Klein

1. COMBINE Klein бутилка и проведе изрязани в средата. Преди това, че се предполага. резултатът е, че две Mobius лента. Това изявление бе потвърдена.

2. COMBINE Klein бутилка, се провежда на ръба на срязване. Преди това те заявиха, че е получил Мьобиус ивица. Това изявление бе потвърдена.

3. COMBINE модел, ние извършихме две разфасовки около ръбовете. Преди това те заявиха, че резултатът ще бъде три Мобиус лента. Това предположение не е била потвърдена. Получената 2 Мьобиус ивица и цилиндъра са получили.

От експериментите, извършвани от нас са следните свойства на бутилката Клайн:

1. Броят на страни - 1.

2. Брой на Бети - това е броят на съкращения, които могат да бъдат направени така, че повърхността не е разделена на две отделни части [2, стр. 507]. От бутилката Klein още няма ръбове (т.е. затворена повърхност), всяка секция трябва да бъде под формата на всяка проста затворена крива, така че Бети номер за нашия модел е 2.

3. хроматичен номер (минимален брой цветове, които могат да бъдат оцветени в модела, така че краищата на всички ребра имат различни цветове) [5, стр. 74]. Klein хроматичната номер шест бутилки. Това означава, че по дадена повърхност 6, могат да бъдат разположени по такъв начин райони с различен цвят на регионите 5 имат обща граница с шестия региона.

4. Бутилка Klein двуизмерен диференцируема колектор неориентируема [6, стр. 208]. Това, за разлика Мьобиус ивица е затворена колектор, т.е. компактен колектор без граница.

5. Не може да се вгражда в триизмерен евклидово пространство E3 (само изпратени), но е вграден в E4.

6. Klein бутилка може да се получи чрез залепване по ръба на два Мьобиус ленти. Но в обикновеното тримерно евклидово пространство E3, това не е възможно без да се създава самостоятелно кръстовища.

Провеждане на експерименти, видяхме след това, какво се случва с бутилката Клайн и направи правилното предположение. Докато първоначално нашите предположения може да не са верни. Значи, това е нашия опит в провеждането на имоти правят изработена повърхността по-достъпни за разбиране.

1. Atanasyan LS Bazylev VT Геометрия. Proc. ръководство за студенти по физика и математика. фактор. симетрични. S-ин. W-2. - М. образование, 1987. - 352 стр.

2. М. Гарднър Математически пъзели и развлечения. - Мир, 1971 - 507 стр.

Основни понятия (генерирани автоматично). Клайн бутилка, бутилка Klein Klein бутилка, Клайн, Клайн бутилка Klein бутилка модел Klein бутилка свойства брой Klein бутилка свойства Klein бутилка, бутилка Klein, триизмерното пространство, Мьобиус банда, хроматични номера диференцируема неориентируема колектор, на експерименти с , триизмерна евклидово пространство, минималният брой цветове, дефинирани неориентируема повърхност, експеримент с рязане, тръбата през отвора.

Ключови думи

Клайн бутилка Мобиус банда, триизмерното пространство на топологични повърхността