Edelennaya натоварване

Когато решението не винаги е практически проблеми може да се приеме, че действа от силата на тялото се нанася в един момент. сили често се прилага към цялата област на тялото (като натоварване от сняг, вятър и т.н.). Това се нарича разпределен товар. Характеризира се с равномерно разпределен товар интензитет р (фигура 1.29). Интензивност - е общото натоварване на единица дължина от конструкцията.

Единицата за измерване на интензитета на [Н / M], [кН / m]. При решаването на проблеми статиката разпределен товар може да бъде заменен с резултантната от които е равна на произведението на интензивността на дължината на част, която действа върху разпределен товар, и който е свързан в средата на тази част.

1.13. Решаването на проблемите на плоска система сили

Пример (фигура 1.30). Определя реакционната просто поддържа силата лъч зареден

и двойка сили с момента М.

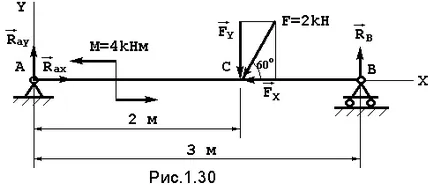
Решение. Ние използваме един и същ план, който е използван за решаване на проблеми в събиращите сили на системата. Целта е да се балансира целия лъч, натоварването, което е показано на чертежа. Капка връзката - на панти А и В. Реакцията на фиксираната шарнир разлага на два компонента -

и, и реакционната смес в подвижната ставата е насочена перпендикулярно на базовата равнина. По този начин, лъч действа плосък произволна система сили, на които е възможно да се направят три равновесни уравнения. Изберете координатна ос и пишете тези уравнения. Уравненията на прогнозите:

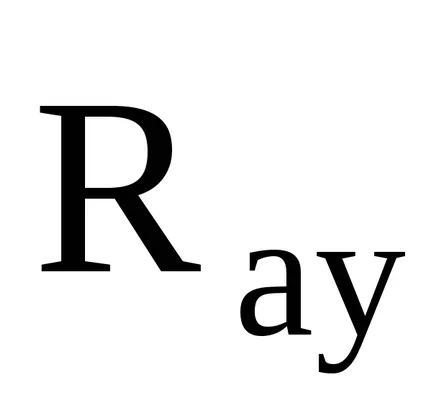
(А чифт издатъци в уравнението не е включена, тъй като сумата на проекциите на двойката сили на всяка ос е нула).

Уравнение момент е по отношение на точка А, тъй като тя се пресича от две неизвестни сили. Ако намерите време по отношение на един чифт точки А не забравяйте, че сумата от моментите на силите по отношение на всяка двойка точки е равно на времето на двойката, и в момента, в знак е положителна, след като двойката се стреми да се завърти по часовниковата стрелка тяло. За да намерите момента на сила

че е подходящо да се разшири вертикалните и хоризонталните компоненти:

и да използвате теоремата Varignon, а трябва да се отбележи, че към момента на сила

спрямо точка А е равно на нула, тъй като насока на действие преминава през тази точка. Тогава уравнението на моменти е под формата:

3.

; RB. 3-FB cos (30) 2 + М = 0.

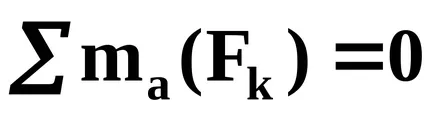
Решаването на това уравнение получаваме:

От уравнение (2) намираме: