детерминанта на разпадане на ред (колона)

Определящо за четвъртата и по-високи заповедите на други често използвани методи за изчисление, отколкото използването на готови формули за изчисляване на определящите фактори за втория и третия поръчките. Един от методите за изчисляване на детерминанти на по-висок ред - използването на разследването на теоремата на Лаплас (теорема самата може да се види, например, в книгата на AG Kurosh "Курс за висше Алгебра"). Това следователно позволява разлагат детерминанта от елементите на ред или колона. В този изчисляване на фактор на п-тия ред намалява за изчисляване на детерминантите на п (п-1) -ти ред. Ето защо тази трансформация се нарича низходящ ред детерминанта. Например, изчисляването на детерминантата на четвъртия ред се свежда до намиране на четирите детерминанти на третия ред.

Да предположим, че са дадени квадратна матрица на п-тия ред, т.е. $ A = \ ляв (\ започне a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \\ \ край \ вдясно) $. Изчислете определящ фактор за тази матрица е възможно, това разширяване на линията или колона.

Ние се определи линия, броят на които е равна на $ I $. Тогава детерминанта на $ A_ $ може да бъде разширена в избран аз-ти ред, като се използва следната формула:

$ A_ $ означава кофактор на елемент $ a_ $ на. За повече информация относно тази концепция Аз препоръчвам да погледнете и темата на кофактор на малолетни и непълнолетни лица. Запишете $ a_ $ е елемент на матрицата или детерминанта разположен в пресечната точка на аз-ти ред J-тата колона. Matrix тема да потърсите повече информация. Видове матрици. Основни понятия.

Да предположим, че искате да се намери сумата от $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $. Какво изречение може да се характеризира с рекордните $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $? Можем да кажем това: това е сумата от звеното на площада, на площада на две, тройки на площада, четирите квадратни и петици квадрат. И може да се каже, че кратко: това е сумата от квадратите на цели числа от 1 до 5. За да се изразят в размер на кратък и служи като записи с използване на писма $ \ сума $ (е гръцката буква "сигма").

Вместо $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $, можем да използваме следния запис: $ \ сума \ limits_ ^ Аз ^ 2 $. Писмо $ аз $ се нарича индекс на сумиране. и номера 1 (първоначалната стойност на $ аз $) и 5 ​​(крайна $ аз $), наречена долни и горни граници на сумиране, съответно.

Дешифрира рекордните $ \ сума \ limits_ ^ аз ^ 2 $ в детайли. Ако $ I = 1 $, тогава $ аз ^ 2 = 1 ^ 2 $, така че първия срок на тази сума е броят на $ 1 ^ 2 $:

Следваща число, след като устройството - две, така заместване $ I = 2 $, получаваме: $ аз ^ 2 = 2 ^ 2 $. Сумата ще бъде, както следва:

След следващия брой 2-3, така заместване $ аз = $ 3 ще бъде: $ I = 2 ^ 3 ^ 2 $. И сумата става:

Остава да бъде заменен само два номера: 4 и 5. Ако заместим $ I = 4 $, $ аз ^ 2 = 4 ^ 2 $ на, и ако ние замени $ I = $ 5, а след това $ I ^ 2 = 5 ^ 2 $. Стойностите на $ аз $ достигнали горната граница на сумиране, така че срокът е 5 $ ^ 2 $ да е последният. Така че, крайната сума в момента е, както следва:

Тази сума може да се изчисли и сълзливо сгънати номер: $ \ сума \ limits_ ^ аз ^ 2 = 55 $.

За практика, се опита да запише и да се изчисли сумата от следните: $ \ сума \ граници _ ^ (5к + 2) $. Индексът на сумиране тук - писмо $ к $, долната граница на сумиране е равно на 3, а горната граница на сумиране е равно на 8.

Един аналог с формула (1) също така съществува за колоните. Формулата за разширяване на детерминанта на й-тата колона е, както следва:

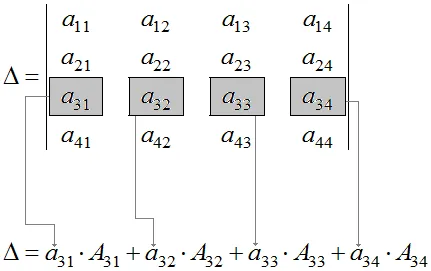
Правилата, изразени от формули (1) и (2) могат да бъдат формулирани както следва: детерминантата е равна на сумата на продукти от някои елементи на ред или колона върху кофактори на тези елементи. За по-голяма яснота, ние смятаме, детерминантата на четвъртия ред, записани в един общ начин:

Ние избираме произволна колона в определящ фактор. Вземете, например, под номер 4. Колоната напише формулата за разлагане на детерминантата на избраната четвъртата колона:

По същия начин, чрез избор, например, на третия ред, се получава разширяване на този ред:

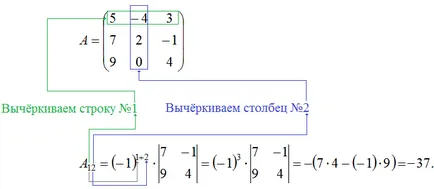
Изчислете детерминантата на матрицата $ A = \ ляв (\ започне 5 -4 3 \\ 7 2 -1 \\ 9 0 4 \ край \ дясно) $, като се използва за разширяване на първия ред и втората колона.

Ние трябва да се изчисли детерминантата на третия ред на $ \ Delta A = \ напусна | \ Започнете 5 -4 3 \\ 7 2 -1 \\ 9 0 4 \ край \ дясна | $. За да го разширят в първия ред, ще трябва да използвате формулата (1). Пишем тази експанзия в общи линии:

За нашите матрица $ a_ = 5 $, $ а _ = - $ 4, $ a_ = 3 $. За да се изчисли кофактори $ A_ $, $ A_ $, $ A_ $ нека използваме формулата №1 на теми, посветени на детерминантите на втория и третия поръчките. По този начин, необходимите кофактори от тях са:

\ започне А _ = (- 1) ^ 2 \ cdot \ напусна | \ Започнете 2 -1 \\ 0 4 \ край \ полето | = 2 \ cdot 4 - (- 1) \ cdot 0 = 8; \\ А _ = (- 1) ^ 3 \ cdot \ напусна | \ Започнете 7 -1 \\ 9 4 \ край \ полето | = - (7 \ cdot 4 - (- 1) \ cdot 9) = - 37; \\ А _ = (- 1) ^ 4 \ cdot \ напусна | \ Започнете 7 2 \\ 9 0 \ край \ дясна | = 7 \ cdot 0-2 \ cdot 9 = -18. \ край

Как да намерите най-кофактори? Покажи \ скрий

За повече информация относно тази концепция Аз препоръчвам да погледнете и темата на кофактор на малолетни и непълнолетни лица. Кратко са изразени в графиката по-долу:

Заместването на получените стойности, записани във формулата по-горе, ние получаваме:

Както можете да видите, намирането на определящ фактор за процеса на третия ред ние намалихме до изчисляването на стойностите на три от детерминанти от втори ред. С други думи, ние намалихме да се започне детерминанта.

Обикновено в такива случаи, обикновена боя не е решение в детайли, отделно намиране кофактори, и едва след това да ги подмените във формулата за изчисляване на определящ фактор. Най-често, просто да води отчет за общата формула - нагоре, докато се получи отговор. Това е начина, по който ще изложи на определящ фактор за втората колона.

Така че, ние се пристъпи към разширяване на детерминантата на втората колона. Спомагателен изчисление няма да доведе - просто продължи формулата, за да получите отговор. Имайте предвид, че във втората колона на един елемент е нула, т.е. $ A_ = 0 $. Това предполага, че терминът $ a_ \ cdot A_ = 0 \ cdot A_ = 0 $. С помощта на уравнението (2) за втората колона за разширение, ние получаваме:

$$ \ Delta А = a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot А _ = - 4 \ cdot (-1) \ cdot \ наляво | \ Започнете 7 -1 \\ 9 4 \ край \ дясна | 2 \ cdot \ напусна | \ Започнете 5 3 \\ 9 4 \ край \ полето | = 4 \ cdot 37 + 2 \ cdot (-7) = 134. $$

Отговорът е получена. Естествено, в резултат на разширяване във втората колона съвпада с резултата от първия ред на разширяването, защото сме изложени на същия определящ фактор. Имайте предвид, че разширяването във втория изчисленията на колоните, които направихме по-малък, тъй като един от елементите на втората колона е равна на нула. Това е така, защото от тези причини за деградация опитайте се да изберете реда или колоната, която съдържа повече нули.

Отговор. $ \ Delta A = $ 134.

Изчислете детерминанта на матрица $ А = \ наляво (\ започне -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ край \ дясно) $, като се използва за разширяване на избрания ред или колона.

За разлагането е най-изгодно да изберете ред или колона, която съдържа общо нули. Естествено, в този случай, че има смисъл да изложи на третия ред, тъй като тя се състои от два елемента, равни на нула. Използване на формула (1). пишем разширяването на определящ фактор за третия ред:

Тъй $ а _ = - 5 $, $ a_ = 0 $, $ а _ = - $ 4, $ a_ = $ 0, горната формула ще се записва, както следва:

$$ \ Delta А = -5 \ cdot A_-4 \ cdot A_. $$

Нека се обърнем към кофактори на $ A_ $ и $ A_ $. За да се изчисли тях ще използва формулата №2 на теми, посветени детерминанти на втория и третия поръчки (в същия този раздел има подробни примери за прилагането на тази формула).

\ започне А _ = (- 1) ^ 4 \ cdot \ напусна | \ Започнете 3 2 -3 -2 \\ 5 1 \\ 7 8 -7 \ край \ дясна | = 10; \\ А _ = (- 1) ^ 6 \ cdot \ напусна | \ Започнете -1 3 -3 \\ 4 -2 1 \\ 9 7 -7 \ край \ дясна | = -34. \ край

Заместването на тези данни във формулата като определящ фактор, ние трябва:

$$ \ Delta А = -5 \ cdot A_-4 \ cdot А _ = - 5 \ cdot 10-4 \ cdot (-34) = 86. $$

По принцип, всички разтвора може да се запише в един ред. Ако пропуснете всички обяснения и междинни изчисления, регистърът на решение ще бъде, както следва:

$$ \ Delta А = a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot А _ = \\ = -5 \ cdot (-1) ^ 4 \ cdot \ наляво | \ Започнете 3 2 -3 -2 \\ 5 1 \\ 7 8 -7 \ край \ полето | -4 \ cdot (-1) ^ 6 \ cdot \ наляво | \ Започнете -1 3 -3 \\ 4 -2 1 \\ 9 7 -7 \ край \ полето | = -5 \ cdot 10-4 \ cdot (-34) = 86. $$

Отговор. $ \ Delta A = 86 $.