Chords Метод - компютърни науки, програмиране
Решение на нелинейни уравнения
Разглеждане на уравнение е (х) = 0, където е (х) - непрекъсната функция с интервал (а, б) производни на първия и втория ред. Коренът се счита за отделен и се съхранява на интервала [а, Ь].
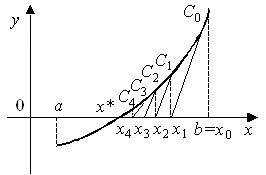
Идеята на хордите на метода е, че при достатъчно малък интервал [а, Ь] дъга на крива у = F (X) може да бъде заменен с хордата и приблизителна стойност на корена вземат точката на пресичане с оста на абсцисата. Да разгледаме случая (фиг. 1), когато първата и втората производни са от същия знак, т.е. F '(х) е ² (х)> 0. уравнение хордата на преминаваща през точките А0 и В, има формата
.
Root сближаване х = x1, за които Y = 0, се определя като
.
По същия начин, за акорд, преминаваща през точките А1 и В следната сближаване се изчислява корен
.
В общ метод формула струни има формата:
Ако първата и втората производни са с различни знаци, т.е.
всички по-близо до основата на х * се извършват от дясната граница на сегмента [а, б], както е показано на фиг. 2, и се изчислява по формулата:
Избор на формулата във всеки отделен случай зависи от формата на F функция (х) и се извършва съгласно правило определена граница интервал е [а, Ь] корен изолация, за които функцията знак съвпада със знака на второ производно. Формула (2) се използва в случаите, когато е (б) е "(б)> 0. Ако неравенството е (а) е" (а)> 0, е целесъобразно да се прилага с формула (3).



Итеративния процес продължава до метод акорд, докато се получи приблизително корен с определена степен на точност. можете да използвате, когато се оценява грешката съотношение на сближаване:
.
След това състоянието на завършеност на изчисление се изписва така:
където д - определено грешки в изчисленията. Трябва да се отбележи, че при определянето на метода на корен акорд често осигурява по-бърза конвергенция, отколкото метода на разполовяване.
4. Метод Нютон (тангенциален)
Нека уравнението (1) има корен на интервала [а, б], където F '(х) и F "(X) са непрекъснато и постоянно знак през интервала [а, Ь].
Геометричната смисъла на метод на Нютон е, че дъгата на крива Y = F (х) се заменя със допирателната. За тази цел, избрани първоначалните предположение Х0 корени в интервала [а, Ь] и се провежда в точка допирателна C0 (x0, F (x0)) на крива у = F (X) до точката на пресичане с оста х (фиг. 3). Уравнението на допирателната в точка C0 на приема формата
Y = F (x0) + F '(x0) х (х - x0).
Освен това, за подход взети корен абсциса X1 на, за които Y = 0:
След това, допирателна линия чрез нова точка C1 (X1, F (х1)) и се определя от неговото пресичане точка х2 с оста на 0x и т.н. По принцип, формулата на метода на допирателната има формата:
В резултат на изчисленията е последователност на приблизителни стойности X1, X2. XI. всеки срок, който е по-близо до корена на х *, отколкото предишната. Итеративния процес се прекратява обикновено когато състоянието (4).
първоначалното приближение x0 трябва да отговаря на условието:
F (x0) е ¢¢ (x0)> 0. (6)
В противен случай, конвергенцията на метода на Нютон не е гарантирана, тъй като тангента пресича абсцисата в точка не принадлежи на интервала [а, б]. На практика, в първоначална корен сближаване x0, обикновено избран една от границите на интервала [а, б], т.е. x0 = А или x0 = б, за които функция марка съвпада със знака на второ производно.
метод на Нютон осигурява конвергенция висока скорост при решаване на уравненията за което стойността на модула на производно ½f ¢ (х) корен ½vblizi достатъчно голяма, т.е. графика на функция у = F (х) има по-голям наклон в близост до основата. Ако крива у = F (X) в интервала [а, Ь] е почти хоризонтална, методът на допирателната прилага не е подходящ.
Значителен недостатък на този метод е необходимостта от изчисляване на производни на организацията за процеса на повторение. Ако стойността е ¢ (х) се променя малко в интервала [а, б], е възможно да се опрости изчисленията използват формула
т.е. стойност на достатъчно производно да се изчисли само веднъж в началната точка. Геометрично, това означава, че допирателните в точки Ci на (XI, F (XI)), където I = 1, 2. заменени от прави линии, успоредни на допирателната към крива у = F (X) в началния момент C0 (x0, F (x0 )), както е показано на фиг. 4.
В заключение следва да се отбележи, че всички по-горе има в случаите, когато първоначалното предположение x0 е избрано достатъчно близо до истинския корен на х * уравнение. Въпреки това, тя не винаги е лесно да се направи. Ето защо, метод на Нютон често се използва в крайния етап на решаване на уравнения, след като работата на надеждна конвергентна алгоритъм, например, методът на разполовяване.
5. Използване на проста итерация
За прилагане на този метод към разтвор на (1), за да го превърне на формата. На следващо място, начално приближение е избран и изчислява x1, x2, а след това и др.:
X1 = J (x0); Х2 = J (х1); ...; XK = J (XK-1).
нелинейни алгебрични уравнения корен
Получената последователност клони към основата при следните условия:
1) J. функцията (х) е диференцируема в интервала [а, Ь].
2) във всички точки на J интервала ¢ (х) отговаря неравенството:
0 £ р £ 1. (8)
При тези условия скоростта на конвергенция е линеен и итерация трябва да се извършва, докато само докато стане на състоянието:
.
,
може да се използва само за 0 £ р £ половина. В противен случай, итерация завършва преждевременно, без да предоставят необходимата точност. Ако изчислението на р е трудно, можете да използвате критерия за края на типа
; ,
Различни методи за превръщане на уравненията (1) на формата. Трябва да се избере едно, което отговаря на условието (8), който генерира конвергентна повтарящ се процес, както е показано на фиг. 5 и 6. В противен случай, по-специално когато ½j ¢ (х) Уг> 1, итерация процес диспергира и не позволява да се получи разтвор (фиг. 7).



Проблемът за подобряване на качеството на изчислителна нелинейни уравнения с помощта на различни методи, като например несъответствие между желаното и реалното, ще има да съществува и в бъдеще. Това решение ще допринесе за развитието на информационните технологии, която се състои в подобряване на методите за организиране на информационни процеси и тяхното изпълнение чрез специфични инструменти - програмни езици и среди.
библиография
2. Abramov SA Зимни EV - Начало на програмирането в Паскал. - М. Science, 1987. -112 стр.
Решение на нелинейни уравнения
Информация за "Решение на нелинейни уравнения"