Център на паралелни сили - studopediya
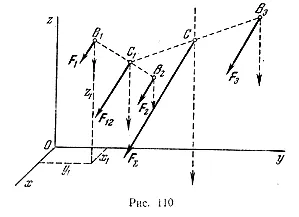
Да предположим, например, орган, прикрепен към точка В1. В2 и В3 три паралелно и удължаване от единия край на F1 на сила. F2 и F3 (фиг. 110). Сгъната първата от съответния-настоящото правило на F1 на две сили и F2. Ние ги намерите ravnodeyst vuyuschuyu-F12. Добавянето след това същото правило със силата на F3 на сила F12, намерете резултатната на F # 931; всички тези три сили. Това очевидно получената пара-данни паралелна сили и насочена в същата посока.
Модулът е сумата на получените състав модула-, регулиращи сили;
Остава да се определи позицията на точка В, през кото-Rui преминава получената линия на действие. За точката на прилагане на получения, разбира се, всеки един момент може да се приема, който се намира на линията на действията си, но се оказва, че само един от тях, а именно точка C, определен от последователно добавяне на сили, има специална, много важно свойство.
Този имот се състои в това, че ако ние се обръщаме всички тези сили около местата за прилагане ъгъл една kovy, без да ги счупи паралелно, а след това им линия на действие на получения включване на същия ъгъл (както е показано на фиг. 110 прекъсната линия niyami) отново ще премине през точка В.
Точка С е известен като център на система от паралелни правителствени сили.
От горното следва, че в центъра на тази система се нарича паралелно точка мощност през която преминава линията на действие на получените сили при всякакво завъртане система около техните точки на прилагане на същия ъгъл в една и съща посока.
Сега се получи формула за определяне центъра координатна система успоредни сили. Вземете система оси пространство-vennuyu и означаване на координатите на точките с данни за прилагане на сили: B1 - x1 съответно. Y, Z1; B2 - x2. y2 z2; B3 - x3. v3. Z3.
Координатите на центъра на паралелни сили означени XC. Нас. ZC.
Както е известно, резултантната сила се казва еквивалент Най тази система на силите, т.е.. E. Полученият прилага при С, към тялото произвежда същия ефект като цялата система на силите F1. F2. Fk ,. Fn. Следователно, съгласно Pierre Varignon теорема, получената момент по отношение на всяка ос е алгебрични сумата на въртящи моменти по отношение на една и съща ос.
Ние дефинираме моментите на сила спрямо оста у.
където к се последователно стойностите от 1 до п.
Следователно, когато определената формула за разделяне на абсциса център паралелни сили се окончателността-ти вид
Определяне на последователността на времето и произтичащите от моментите-ви на всички компоненти на силите около оста х, ние откриваме, че F # 931; YC = # 931; Fh YK, където формулата за определяне на съгласува цента-ра паралелни сили
Подобен формула за трети координират (applicate) център паралелни сили
се получава, ако всички сили се въртят от 90 °, например, така че те са разположени успоредно на оста у, и се определят моментите на сила от оста х в относително.
Следователно, паралелни сили на център координати формула са на формата
където Fh - модули паралелно сила, ХН. ук. ж - координати на точките на тяхното прилагане.