Броят на различните K-подгрупи на елементарни N-елементарни комплекти - studopediya

Нека сега да видим, тъй като има различни подгрупи на к елементи на снимачната площадка, състояща се от наш елементи (к <п).

TeoremaChislo различни к-н-елемент подгрупи на групата се равнява на елементарните

където намаляване н! = N * (п - 1) *. * 3 * 1 * 2 факторен нарича номер п (п четима факторен). А 0! = 1. редукция.

Доказателство. За конструиране на к-елемент подмножество на А, е необходимо да се (к - 1) елемент в набор за свързване на един от N - к + 1 елементи, които не са включени в тази подгрупа. Тъй като броят на (К - 1) елемент в подгрупи на същото, и всеки един от тези подгрупи може да бъде к-елемент п - к + 1 начини, основното правило на комбинаторна номер Toriki се * (п - к + 1) подгрупи. Въпреки това, не всички от тези подгрупи са различни, тъй като всеки к е елементарна подгрупа също може да се изгради к начини. Ето защо,

Тъй - броя на лъжливо подгрупи А - е равна на N, тогава

Произволното к-елемент подгрупа А се нарича комбинация, или проба, а броят - броят на комбинации или комбинации от п елементи от к елементи.

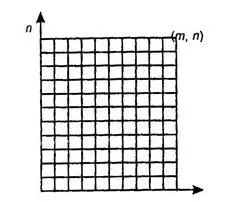
Биномен коефициент имат интересен геометрична Interprom-tatsiyu. Нека да има правоъгълна шахматна дъска размер м от п, времеви преместванията в координатната равнина. Този съвет се състои от m * п елементарни квадрати разделени с п - 1 Hori-тал линия и m - 1 вертикална. Определяне на броя на различни кратки пътеки може да се стигне от точка (0, 0) до точката (т. N) на този форум.

Всяка краткия път, водещ от точката (0, 0) в точка (m, п), очевидно се състои от М + п Гарнитура елементарни квадрати, сред които m Hori-zontally и п вертикално. Тези пътища се различават само една редица вертикални и хоризонтални страни. Следователно, общият брой пътеки е равен на броя на начините, по които на м + н страни могат да избират п-вер-местни, т.е. този номер е.

Имайте предвид, че не може да се разчита на вертикалните страни,

както и в хоризонтално положение. Това означава, че има голямо разнообразие от най-кратките маршрути и следователно равенството:

Това равенство се нарича "формула на симетрия."

От тази формула, ние имаме в резултат на:

като от заглавието "добавянето на формула". Ние доказваме, този ефект.

Комбинираното екип на университета волейбол работят 15 души. Колко различни опции трябва да обмисли треньора преди мача да обяви списъка с играчи в играта?

Решение: Броят на играчите на екипа по волейбол е шест. Следователно, броят на всички възможни варианти - редица различни подгрупи, състояща се от шест елемента в набор от петнадесет елементи. По този начин, от Теорема 2 имаме