Antiderivatives

Вид работа: 7
Относно: примитивните функции

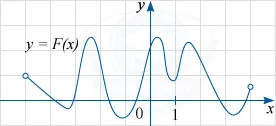
Фигурата изобразява графика на функция у = F (х) - един от примитивите на определена функция е (х). определена на интервала (-5, 5). С помощта на модела, определя броя на разтвори на F в уравнение (х) = 0 в интервала [-3; 4].

Според определението на примитивни, равенството: F '(х) = F (х). Следователно, F в уравнение (х) = 0 може да бъде написана на форма F '(х) = 0. Както е показано на Фигура графика на у = F (х), е необходимо да се намери точките на интервала [-3; 4], при което производното на функцията F (х) е нула. Фигурата показва, че това ще абсцисата крайни точки (максимална и минимална) на графиката F (х). Тяхната в споменатия интервал точно 7 (четири точки на минимум и максимум на три точки).

Вид работа: 7
Относно: примитивните функции

Фигурата изобразява графика на функция у = е (х) (която е начупена линия, съставена от три праволинейни сегменти). С помощта на модела, изчисли F (5) -F (0), където F (х) - един от примитиви функция F на (X).

Според формула основните теорема разлика F (5) -F (0), където (х) F - един от примитиви функция F на (х), равна на площта на кривата трапец ограничена график функция у = е (х), у = 0 права , х = 5 и х = 0. От графиката се установим, че каза криволинейни трапец е трапец с основа, равна на 5 и 3 и височина 3.

Площта му е равна на \ Фрак \ cdot 3 = 12.

Вид работа: 7
Относно: примитивните функции

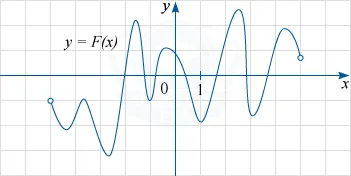
Фигурата изобразява графика на функция у = F (х) - един от примитивите на определена функция е (х), определена на интервала (-5, 4). С помощта на модела, определя броя на разтвори на F в уравнение (х) = 0 в интервала (-3, 3].

Според определението на примитивни, равенството: F '(х) = F (х). Следователно, F в уравнение (х) = 0 може да бъде написана на форма F '(х) = 0. Както е показано на Фигура графика на у = F (х), е необходимо да се намери точките на интервала [-3; 3], в която производното на функцията F (х) е нула.

Фигурата показва, че това ще абсцисата крайни точки (максимална и минимална) на графиката F (х). Тяхната в споменатия интервал точно 5 (две точки на минимум и максимум на три точки).

Вид работа: 7
Относно: примитивните функции

Фигурата показва графика на функция у = е (х). функция F В (х) = - х ^ 3 + 4,5x ^ 2-7 - един от примитивите на функцията F (х).

Намерете лицето на защрихованата фигура.

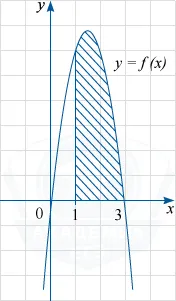
Защрихованата фигурата е извита трапец ограничена горе графика на у = е (х), прави линии у = 0, X = 1 и х = 3. Съгласно формулата за основните теорема от площта S е равна на разликата между F (3) -F (1), където F (х) - в споменатия субект примитивна функция е (х). Следователно, S = F (3) -F (1) = -3 ^ 3 + (4,5) \ cdot 3 ^ 2 -7 - (- 1 ^ 3 + (4,5) \ cdot 1 ^ 2 -7) = 6,5 - (- 3.5) = 10.

Вид работа: 7
Относно: примитивните функции

Фигурата изобразява графика на функция у = е (х). функция F В (х) = х ^ 3 + 6x ^ 2 + 13x-5 - един от примитивите на функцията F (х). Намерете лицето на защрихованата фигура.

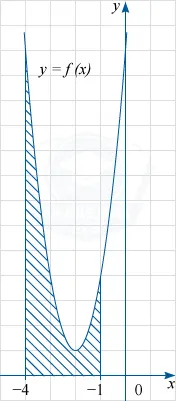
Защрихованата фигурата е извита трапец, ограничена от графиката на у = е (х) и прави линии Y = 0, X = -4 и х = 1. Съгласно формулата за основните теорема от площта S е равна на разликата между F (-1) -F (-4), където (х) F - в споменатия субект примитивна функция е (х).

Вид работа: 7
Относно: примитивните функции

Фигурата показва графика на функция у = е (х). Функцията F (х) = х ^ 3 + 18x ^ 2 + 221x- \ frac12 - един от примитивите на функцията F (х). Намерете лицето на защрихованата фигура.

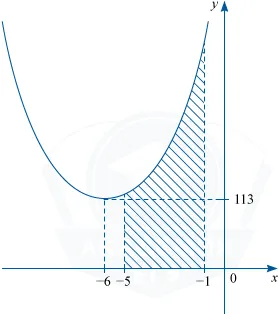
Между основните теорема формула S = F (-1) -F (-5).

F (-1) = (-1) ^ 3 + 18 \ cdot (-1) ^ 2 + 221 \ cdot (-1) - \ frac12 = -204- \ frac12.

F (-5) = (-5) ^ 3 + 18 \ cdot (-5) ^ 2 + 221 \ cdot (-5) - \ frac12 = -125 + 450-1105- \ frac12 = -780- \ frac12.

F (-1) -F (-5) = -204- \ frac12- \ наляво (-780- \ frac12 \ дясно) = 576.

Вид работа: 7
Относно: примитивните функции

Фигурата показва графика на функция у = е (х). С помощта на модела, изчисли F (9) -F (3), където F (х) - един от примитиви функция F на (X).

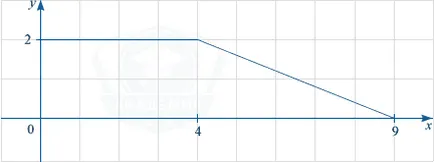
F (9) -F (3) = S. където S - площ на фигурата, ограничена от графиката на функция у = е (х), прави линии у = 0 и х = 3, \ = 9 х. Да разгледаме следния фигурата.

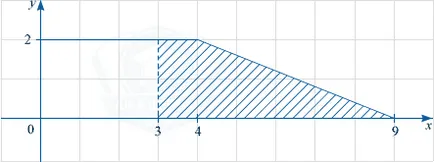
Тази цифра - трапец с основи 6 и 1 и 2. Неговата височина е равна на район \ Frac \ cdot2 = 7.

Вид работа: 7
Относно: примитивните функции

В графиката на функция у = е (х) показва координатна равнина. Един от примитиви тази функция има формата: F (х) = - \ frac13x ^ 3- \ frac52x ^ 2-4x + 2. Намерете лицето на защрихованата фигура.

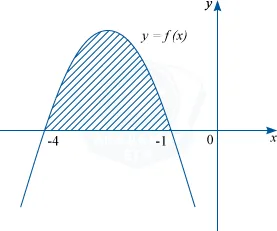
Фигурата показва, че излюпени фигурата, ограничена по абсцисата точки -4, -1. и ордината графиката на функцията: е (х). Така площ от фигурата, можем да намерим разликата с помощта на примитивите стойности в точките -1 и -4. съгласно формулата на определен неразделна:

Заместник стойността на примитивни условия и да получат областта на фигурата:

Вид работа: 7
Относно: примитивните функции

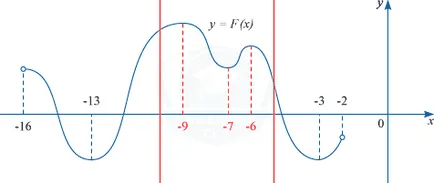
Примитивни на у = F (х) на функция у = е (х) се определя на интервала (-16, -2). Определи колко решения е уравнението F (х) = 0 в интервала [-10; -5].

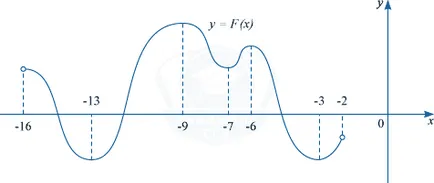
Формулата на примитивни е както следва:

Според проблем да се намери точката, в която F функция (х) е нула. Като се има предвид примитивна формула, което означава, че трябва да се намери точката, в която F '(х) = 0. т.е. точките, в които производното на примитивни е нула.

Ние знаем, че производната е нула в точките на локален екстремум, т.е. функция има разтвори в тези точки, при което увеличението на F (х) се заменя със спад и обратно.

В интервала [-10; -5], може да се види, че тази точка: -9; -7; -6. Следователно уравнение е (х) = 0 има три решения.