алгоритмичен състав

Теорията на хаоса е разработен от френския математик Анри Puankare в началото на XX век. Теорията на хаоса - математически апарат описание на поведението на някои нелинейни динамични системи, при спазване на определени условия, когато един феномен, известен като хаос. Поведението на такава система изглежда е случаен, дори и ако моделът описва системата е детерминирана. За да се подчертае особеното естество проучен в рамките на тази теория на явлението общоприето да се използва името на динамичната теория на хаоса.

Примери за такива системи включват атмосферата, сътресения, някои видове сърдечни аритмии, биологични популации, обществото.

Един добър пример за динамична система - просто махало. Нейната движение се определя от само две променливи: положение и скорост. По този начин, неговото състояние - това е точката, в самолета, чиито координати - позицията на махалото и скорост. Evolution състояние правило е описано, който е получен от закон на Нютон и се изразява математически като диференциално уравнение. Когато махалото напред и назад, неговото състояние, на мястото на ходовете равнина по протежение на пътя ( "орбита"). В идеалния случай без триене махало орбита е контур, с триене орбита спирали до точка, съответстваща на спиране на махалото.

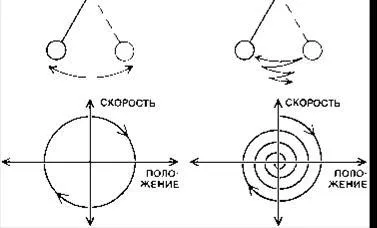
махалото като динамична система с орбита

Хаотични системи са разделени на разсейване (стационарно състояние, се появява в условие разсейване nonequilibrium среда (дисперсия) на енергия, който е снабден от външната страна) и запазена (икономия на енергия). В природата, най-често срещаните дисипативни системи.

Тъй като тези системи непрекъснато губят енергия и тяхната фаза пространство, т.е. пространствената област, където система - се превръща в определено състояние който се нарича атрактор на системата. Атрактори - геометрична структура, които характеризират поведението на системата във фаза пространство след като дълго време. Грубо казано, един атрактор - това е нещо, че системата има тенденция да се стигне до това, което тя е привлечена. Attractor може да бъде една точка или набор от точки. Към хаотична система се прилага известен "пеперуда ефект", описан от Едуард Лоренц. Всяка малка промяна в първоначалните стойности на променливите на системата е напълно различна последователност на изходните стойности.

На следващо място, погледнете основните видове хаотични системи и да се опита да направи картографиране на симулирания с помощта на нелинейни уравнения на числени стойности в пространството на музикални събития.

Математическите уравнения, описващи поведението на хаотични системи парадоксално проста - те са известни като не-линейни уравнения, т.е., с безкраен брой решения.

Едномерна хаотични системи

Логистичен уравнение за първи път е въведена от белгийското социолог и математик Пиер Франсоа Verhulst през 1845, за да се симулира нарастването на населението:

Ключов параметър в това уравнение е - той определя поведението на системата в дългосрочен план. Изходните стойности логистично уравнение зависят от стойността - за по-малко от 3, системата се стабилизира на същата стойност. С нарастване - от двете стойности, и така нататък до достигане на критичната стойност на 3.569946, когато системата става непредсказуем. По същия начин, като пространството на две октави музикални събития, можем да възложи на изходните стойности на някои бележки. Например, като а = 3.3, ние откриваме, че системата се колебае между 0,48 и 0,82, което е равно на повторение на две бележки, като четири - ние се непредсказуемо хаотичното движение на системата между 0 и 1, което е много по-подходящ за подготовката на мелодии.

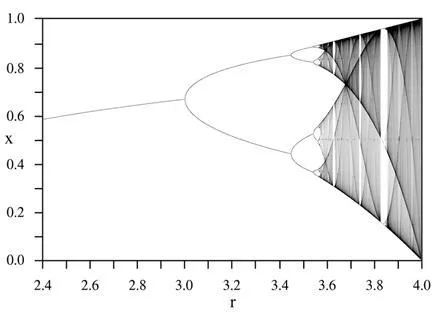
бифуркация диаграма. Всяка вертикална привличаща сектор показва определена стойност. Диаграмата показва удвояването на периода, когато се увеличава, което в крайна сметка води до хаоса

Двумерен хаотични системи

Henon носи името на своя откривател Мишел Henon, френски астроном. Това привличаща не описва всяко физическо явления и е създадена като двуизмерен модел за разсейване хаотични системи. То се изразява със следните уравнения:

За картографиране двуизмерни параметрите космически атрактори в музикални събития, предлагани в следната последователност от действия. Тъй като всяка итерация дава нова стойност за това, изборът е или да присвоите различни музикални параметри на тези променливи, като музика и продължителност, или в комбинация от две променливи, една стойност - разстоянието от първоначалните координатите на текущата точка на атрактор на формулата:

След получаване на дълга поредица от стойности, можем да се изчисли честотата на възникване на някои бележки и въз основа на това да направи мелодия. Прави впечатление, че разпределението на оценка за картографиране на двуизмерни атрактори параметри дава разпределение, това е подобно на Гаус.

странни атрактори

В допълнение към тези редовни атрактори съществуват странни атрактори. Странното атрактор - това привличаща като две основни разлики от конвенционален привличаща: привличаща траектория като nonperiodic (тя не е затворен) и режима на работа е нестабилна (малки отклонения от режима на бране). Основният критерий за хаотичен атрактор е експоненциалното нарастване на малки сътресения от време. Последицата от това е "смесване" на системата е апериодична във времето на всеки от координатната система, непрекъсната мощност спектър и намаляване на автокорелационната функция на времето.

Така привличаща е Lorenz привличаща описано три уравнения, и съответно са триизмерен: