Алгебра 10 клас

Въпрос: Какви са те измерва? Те измерва съотношението на броя на събитията, които се падане на герб (означена с буквата М) на броя на изпитвания (означена с буквата N). Съотношението m / п се нарича относителната честота на събитието. Но се получава горното определение на вероятност (фиг. 8, поз. 1). Сега затегнете вашите мозъци, преди да кликнете върху въпроса.

Каква е разликата между понятията "относителната честота на събитието" и "вероятност на събитието"?

Вероятност на събитие се изчислява теоретично, докато разглежда възможните случаи на единична експеримент. Относителната честота на събитие се измерва почти едновременно произвежда голям брой експерименти.

Практиката показва, обаче, че когато голям брой експерименти относителната честота на събитието обикновено е малко по-различна от вероятността. И толкова по-голям броя на експериментите, стойността на тяхната по-близо. Често не е възможно да се изчисли вероятността на събитието. След това, когато има достатъчен брой експерименти, относителната честота на събитието може да се счита като приблизителна стойност на вероятността.

предизвикателно преживяване

Нека произведени няколко независими експерименти. Експериментите се наричат ​​независими, ако резултатът от всеки един от тях не зависи от резултата в други експерименти. Тези серии опити наричат ​​трудно преживяване. Има много задачи в които трябва да се определи вероятността от определена комбинация резултати в комплекс опит. Например, дори направи предизвикателно преживяване, което се състои в това, че на първия флип монета и след това хвърли заровете. Трябва да знаем, че вероятността спад палто (наричаме това събитие А), но във втория план от същия комплекс опит куб попада 3 точки (наричат ​​това събитие б) в първия експеримент, сложен опит. Вероятността, че в първия експеримент попада гребен равно на 1/2 (P (A) = 1/2), вероятността, че попада във втория експеримент 3 точка се равнява на 1/6 (P (B) = 1/6). Вероятността от комбинацията на тези събития е равна на (1/2) (1/6) = 1/12.
Р (А, В) = Р (А) P (B)
Тази формула може да се обобщи до п независими проучвания: P (А1 А2 Един ..) = Р (А1) P (А2). P (AN).
Например, хвърля монета четири пъти, и ние трябва да знаем вероятността, че всички 4 пъти попадат палто. Вероятността, че всеки отделен опит ще падне емблема е 1/2. (1/2) (1/2) (1/2) (1/2) = (1/2) 4 = 1/16

Бернули формула. Законът за големите числа.

Нека опита на (нека го наречем просто) вероятност на събитие е равна на стр. Тя произвежда предизвикателно преживяване, състоящ се от п прости експерименти. Резултатът във всеки прост експеримент не зависи от резултата от други прости експерименти. Тогава вероятността да се окаже трудна опит Ak събития. състоящ се в това, че едно събитие А настъпва к пъти (к е не повече от п), равна на (бавно и внимателно проучване на формулата на фиг. 11). Моля, имайте предвид, че обикновено вместо Pn (An) напиши Pn (к). Формулата на фиг. 11 се нарича формула Бернули.

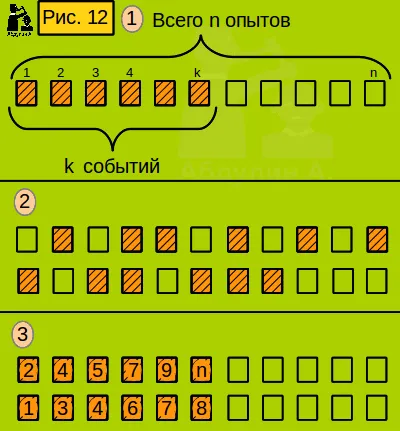
Но това е може би само в резултат на сложен опит. Но има и други възможни резултати, когато събитието A настъпили в други прости експерименти, но броят на събитията в трудна опит А също е равна на к. Някои I са представени на фиг. 12, поз. 2 вероятност за такъв резултат е същото като това, което обсъжда. Ето защо, ние трябва да намерим броя на възможните резултати от комплексна опит.

По-рано в тази работа има раздел за комбинацията. Прочетете го, ако забравя. Броят на резултатите е броят на комбинациите от п на к. За яснота, I са представени някои от възможните комбинации на фиг. 12 Поз. 3. Това е същата комбинация че в позиция 2.

Увеличи броя на възможните резултати в вероятността за всеки изход. Ние получаваме формулата на фиг. 11.

Обърнете внимание на формулата на фигура 13. Тя изразява номера първи собственост Pn (K): за всяко положително цяло число N, сумата на всички числа Pn (к) е равен на 1. За тези, които не разбират, обясни популярен. Комплексът преживявания, състоящи се от п прости експерименти събитие могат да се появят к пъти, където к е числото от 0 до п. Ако добавим и вероятността, че едно събитие да се случи к пъти, за kazhogo на възможните стойности на к (0 до н), се получи един. Ако си мислиш за него, става очевидно. Unit - вероятността за дадено събитие, в този случай сложен опит.

Преди да се изясни номера втори собственост Pn (к), са два примера за урок Николски. Таблицата показва приблизителни стойности на P10 (к) за р = 1/5 За тези, които не разбират: р - е вероятността на събитието по прост експеримент, к - броят на такива събития в трудна опит, P10 (к) - вероятността предизвикателно преживяване от 10 прости експерименти събитие ще настъпи к пъти.

И в двете таблици, стойността на Pn (к) се увеличава, достига максимум и след това отново отива в упадък. к, стойност. където Pn (к) maksmialna приблизително равна на NP, NP + 1 пъти. В първия пример, NP = 10 (1/5) = 2. Sootvetvenno Pn (к) е максимален при к = 2. Във втория пример, NP = 6 (2/3) = 4. Sootvetvenno Pn (к) е максимален при к = 4. Моля, имайте предвид, че ръбовете на маси, с минимален и максимален к, стойностите на Pn (к) е малък. Най-високи стойности на Pn (к), скупчени около максимума. Тези закони представляват номера втори собственост Pn (к). За тези, които не разбират, че дъвче: Например, вероятността на събитието по прост процес е стр. Тя произвежда предизвикателно преживяване, sootoyaschy на п прости експерименти. След това, максимална вероятност, че този труден опит на събитието ще се случи време NP (в някои случаи, NP + 1 пъти). Шансовете са, че събитието ще се случи NP + 1 път или NP-1 пъти. Вероятността, че дадено събитие ще се случи по-няколко пъти, много по-малко, и колкото повече броя е различен от NP, толкова по-малко. В Николски учебник дава в подкрепа на този закон математически изчисления. На кого му пука себе сваляне на файлове и се рови.