аксиален вектор

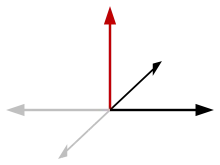
След обръщане на двата вектора промените знак, но тяхната вектор продукт остава непроменена.

Аксиални вектор (аксиална централна Engl ..) или псевдо - количество чиито компоненти се превръщат с вектора ротации на координатната система, но променя знак е противоположна на поведението на компонентите на вектора на всеки инверсия (циркулация знак) координати. Т.е. псевдо обръща при запазване на абсолютната стойност на (се умножава по минус едно) по всяко инверсия на координатната система.

За да се подчертае разликата между настоящото вектор, чиито координати винаги се превръщат както и координатите на вектор за движение, този вектор се нарича вярно или полярен вектор.

Най-простият пример на аксиален вектор в триизмерното пространство е вектор продукт на вектори на две полярности, например, в механиката - ъглов момент L = R х р = \ mathbf \ пъти \ mathbf

>. в четириизмерното пространство - аксиален ток.

Когато координатна трансформация координира аксиално вектор, получен чрез умножаване допълнителен фактор (-1) в сравнение с истинския координатна трансформация (наречена друго полярни) вектори, ако основа променя ориентацията (например, ако основата се подлага на огледално отражение). Това, заедно с pseudoscalar. специален случай на псевдо. Графично е представена в тази псевдо-координират сменя посоката на климата.

• Геометрията на най-широко използваната представителство заявление pseudovec- може да бъде с помощта на триизмерен безкрайно малко въртене. Вероятно (?), Вектор Терминът аксиален е именно тук, тъй като псевдо определя ос на въртене (неговата посока), но само с фактор (± 1), с посоката на въртенето на свързания с условна произволен избор на правилната основа, за разлика от истинската ( полярен) вектор представлява насочена сегмент (или паралелно превод) съвсем ясно и недвусмислено посочено начални и крайни точки.

Обичайният начин за генериране на pseudovectors pseudovectorial тази операция, най-често, ако не е единственият, обикновено се използва в триизмерен случай е вектор продукт (както е обичайно в координатната нотация включва Леви-Civita псевдо) експлоатация и съдържащ вектор продукт (например, ротор и т.н. ). или нечетен брой от тях. операция Pseudovector генерира вярно на вектори и Scalars pseudovectors и pseudoscalars.

Така че, когато умножена по истински вектора на истинската вектор - се получава скаларен продукт истински скаларна и вектор продукт - псевдо. Когато се умножи вектор от истински pseudoscalar продукт се получава в pseudoscalar и вектор продукт на истински вектор. Когато се умножи две pseudovectors - получени съответно вярно скаларна и псевдо.

Физическите теории, с изключение на тези, в които има различни и наблюдавани по принцип огледалната симетрия пространство pseudovectors могат да присъстват в междинните стойности, но в последните наблюдавани - мултипликатори (-1) в огледално отражение на координати трябва да бъдат унищожени, среща в работи дори брой пъти (четен брой + pseudovector pseudoscalar + pseudotensorial други фактори).

• Например, в класическата електродинамика магнитна индукция - псевдо са били генерирани псевдо операция, например й х г \ пъти \ mathbf \> право Biot-Savart. но стойността на тази (псевдо) определя по принцип до условно множител, който може да бъде избран един или -1. Въпреки това, действителната наблюдаваната стойност - такса ускорение под въздействието на магнитното поле - ако изчисляването му се състои от друга операция pseudovector о × B \ пъти \ mathbf \> в израз за силата на Лоренц. давайки още един условен фактор ± 1, равна на първата, отговорът е произвол изчезва, тъй като продуктът на ± 1 · (± 1) дава 1.
• Механиката на pseudovector най-често срещащи стойност - ъглова скорост и свързаната (например, ъглов момент). вектор вярно скорост се получава от pseudovec- ъглова скорост ω \> псевдо операция ω х R \ пъти \ mathbf \>.