9) разтвор на неопределени система линейни уравнения

Системата на m линейни уравнения с п неизвестни (или линейна система, използва съкращението SLAE) в линейната алгебра - система от уравнения на формата

Съвместно SLE - SLU, има един или повече решения.

Несигурно SLE - съвместен SLU, която има повече от едно решение.

Разрешени от Йордания - Гаус. Решения се изразяват с помощта на свободни условия.

10) хомогенни линейни уравнения

Slough се нарича хомогенна, ако всички негови постоянни условия равна на 0.

Теорема 1 (на нетривиални разтвори на хомогенна система)

Хомогенна линейна система с квадратна матрица има nontrivial решение, ако и само ако детерминанта е нула.

Доказателство за теорема Cramer, ако и само ако системата има уникален квадратен разтвор матрица (т.е. вектори - Колони система - е линейно зависим). Ако имаме система от линейни уравнения хомогенни, разтворът - тривиално (0,0, ... 0). Така че, има нетривиални решения единствено и само ако (т.е.. Един безкраен набор от решения).

Всеки разтвор БАВНО изразена като линейна комбинация

, ...,.

Ние показваме, че векторът - линейно независими. За тази композиция matritsuiz техните координати:

.

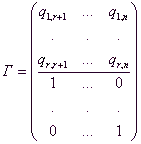
Намира се под непълнолетния на ред, различен от nulyastolbtsov matritsylineyno независими.

Следователно вектори - са линейно независими, т.е. Тези вектори образуват основа на подпространството.

Кондиционира тривиално съвместимост:

Към хомогенна система има nontrivial решение, ако и само ако ранга на основната му матрица е по-малко от броя на неизвестни

Kronecker - Capelli - критерия за съвместимост на системата от линейни алгебрични уравнения:

Системата на линейни уравнения е съвместима единствено и само ако ранга на основната му матрица е равен на ранга на своя разширената матрица, със системата има уникално решение, ако в ранг е равен на броя на неизвестни и безкраен брой решения, ако ранг е по-малко от броя на неизвестни.

11. вектори. Линейни операции на вектори

Геометрична вектор (или вектор) се отнася сегмент.

Векторът се нарича нула, ако в началото и края на мача си. нула

вектор не е определена посока и има дължина, равна на нула. това

Тя позволява записването за идентифициране на вектора нула до реално число

Вектори се наричат ​​колинеарни, ако те лъже или на едно-

Ной линия или на успоредни линии.

Две вектори се казва, че е равна, ако те лежат на една права, са odi-

Накова дължина и съща посока.

Линейни операции на вектори.

Linear операция, наречена операция на вектор допълнение и ope-

радио вектор умножение от реални числа.

сума от А + В на два вектора на А и В е вектор за удължаване

вектор от произхода до края на вектор В с уговорката, че вектор б

прикрепен към края на.

1. А + В = б + а (Комутативност);

2. (А + В) + с = а + (б + в) (асоциативност);

Разлика а - б на вектор и вектор б се нарича вектор

в, която е вектор на сумата б получава вектор.

А α продукт (или aα) вектор на реално число α

Това е вектор б, колинеарни вектор, имаща дължина

равно на | α | · | а |. и с посока, съвпадаща с посоката

Niemi вектор, в случай на α> 0 и обратна посока

вектор, в случай на α <0.