zhegalkin полином

Zhegalkin полином - полином над пръстен $ \ mathbb_2 $ на, която е полином с коефициенти на формата 0 и 1, където продуктът се приема като връзка, и като допълнение - XOR. Полиномен беше предложена през 1927 г. от Иван Zhegalkin като удобен начин за представяне на булеви функции. Във външната литература представяне във формата на полином Zhegalkin обикновено се нарича алгебрични нормална форма.

Теорема Zhegalkin - твърдение за съществуването и уникалността на изображението на всеки булева функция като полином Zhegalkin.

Zhegalkin полином е сумата по модул две произведения от обърнатата променливи и константи

Формално Zhegalkin полином може да се запише като

или в по-формализирана като:

$ P = а \ oplus \ bigoplus_1 \ екв i_1<\ldotsa_ \ клин x_ \ клин \ ldots \ клин x_ \ четириядрен един, a_ \ инча $

Примери на полиноми Zhegalkin:

$ P = B \ oplus AB; $
$ P = X \ oplus YZ \ oplus ABX \ oplus ABDYZ; $
$ P = 1 \ oplus A \ oplus ABD. $

Според теоремата на тази публикация, че системата на булеви функции е пълна, че е необходимо, че съществуват

Най-малко една функция, не спести $ 0 $;
Най-малко една функция, не спести $ 1 $;
Поне една нелинейна функция;
Най-малко един не-монотонна функция;
Най-малко един nesamodvoystvennaya функция.

Въз основа на това, системата на функциите $ \ bigl \ langle \ клин, \ oplus, 1 \ bigr \ rangle $ е пълна:

Въз основа на тази система и полиноми Zhegalkin построена.

Съществуването и уникалността на представяне

Zhegalkin теорема: Всеки Булева функция може да се представи по уникален начин като полином Zhegalkin.

Имайте предвид, че различни булеви функции на $ N $ променливи $ ^ $ 2 бр. В този вид съюзи $ x_ \ ldots x_ $ има точно $ 2 ^ п $, защото на $ N $ възможни фактори, или всяка част от съюза, или не. В полинома при всяка такава съюзи струва $ 0 $ или $ 1 $, т.е., има 2 $ ^ $ Zhegalkin различни полиноми на $ п $ променливи.

Сега е достатъчно да се докаже само, че различните полиноми изпълняват различни функции. Да приемем, напротив. След това се равнява на две различни полином и преместване на един от тях от другата страна на уравнението, получаваме полинома идентично нула и има ненулеви коефициенти. Тогава помисли за срока с един коефициент на най-малката дължина, която е с най-малък брой променливи, които участват в него. Заместването на единица на мястото на тези променливи, и нули в останалите места, ние откриваме, че този комплект е само един мандат отнема една стойност, която е равна на нула на един от наборите е 1, е противоречие. Следователно, всеки Булева функция изпълнява от полином Zhegalkin еднозначно.

Сграда Zhegalkin полином

Има няколко начина за изграждане на Zhegalkin полином.

Според таблицата на истината

Нека F функцията $ (x_1, x_2 \ точки, x_n) $ е дадена таблица истина. Пишем тази първа функция като Zhegalkin полином с неопределен коефициенти. След това един по един заместител на всички видове комплекти, за да се увеличи броят на единиците и да намерят коефициентите предвид факта, че долара \ oplus 1 = \ бар $ и $ на \ oplus 0 = а $. За всяка пермутация ние откриваме само един коефициент.

Пример: дадена функция $ е (x_1, x_2, x_3, x_4) $ и истина таблица:

Ние построи за нея полином Zhegalkin:

$ F (x_1, x_2, x_3, x_4) = a_ \ oplus a_ x_1 \ oplus a_ x_2 \ oplus a_ x_3 \ oplus a_ x_4 \ oplus a_ x_1 x_2 \ oplus a_ x_1 x_3 \ oplus a_ x_1 x_4 \ oplus \\ \ oplus a_ x_2 x_3 \ oplus a_ x_2 x_4 \ oplus a_ x_3 x_4 \ oplus a_ x_1 x_2 x_3 \ oplus a_ x_1 x_2 x_4 \ oplus \\ \ oplus a_ x_1 x_3 x_4 \ oplus a_ x_2 x_3 x_4 \ oplus a_ x_1 x_2 x_3 x_4 $

Тъй $ е (0,0,0,0) = 0 $, след $ a_ = 0 $.

След това, ние да замени всички други групи във възходящ ред на броя на дяловете, чрез заместване на новите стойности, получени в следната формула:

$ F (1,0,0,0) = a_ \ oplus a_ = 1 \ стрелкаНадясно a_ = $ 1

$ F (0,1,0,0) = a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (0,0,1,0) = a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (0,0,0,1) = a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (1,1,0,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ стрелкаНадясно a_ = 0 $

$ F (1,0,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = $ 1

$ F (1,0,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = $ 1

$ F (0,1,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ стрелкаНадясно a_ = $ 1

$ F (0,1,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (0,0,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (1,1,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ стрелкаНадясно a_ = 0 $

$ F (1,1,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 0 $

$ F (1,0,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ стрелкаНадясно a_ = 0 $

$ F (0,1,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = 1 $

$ F (1,1,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus \\ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ стрелкаНадясно a_ = $ 1

По този начин, полином Zhegalkin изглежда така:

$ F (x_1, x_2, x_3, x_4) = x_1 \ oplus x_1 x_3 \ oplus x_1 x_4 \ oplus x_2 x_3 \ oplus x_2 x_3 x_4 \ oplus x_1 x_2 x_3 x_4 $

Превръщането на разделителния нормална форма

Този метод се основава на факта, че $ X \ oplus 1 = \ бар $. Ако функцията се определя като DNP, е възможно първо да премахнете дизюнкцията, използвайки правилото Де Морган и всичко отказ замени добавяне на един модул две, а след това отворете скобите, както обикновено, като се вземе предвид, че четен брой на равни условия е равна на нула, а нечетен брой и същи стоки се равнява на една такава summand. Или можете да замените дизюнкцията по следния начин: $ A \ боже B = AB \ oplus A \ oplus B $ $ (1) $.

Ако функцията е дефинирана в PDNF, а след това, тъй като за всяка стойност на входните променливи в устройството не се справя повече от един член на израза, а след това просто да замени всички изключителни или дизюнкцията.

Пример: Dan функция в DNF $ е (x_1, x_2, x_3, x_4) = (x_1 \ земя x_2 \ земя \ отр x_3 \ земя x_4) \ LOR (\ отр x_1 \ земя \ отр x_4) \ LOR (x_1 \ земя x_2) \ боже x_2 $, изграждане Zhegalkin полином.

Пишем функцията по следния начин:

$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ отр x_3 x_4 + \ отр x_1 \ отр x_4 + x_1 x_2 + x_2 $;

Група трансформация условия и използване (1):

$ F (x_1, x_2, x_3, x_4) = (x_1 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 \ отр x_4 \ oplus x_1 x_2 \ отр x_3 x_4 \ отр x_1 \ отр x_4) + (x_1 x_2 \ oplus x_2 \ oplus \ oplus x_1 x_2 x_2) $

Ние използваме свойствата на връзка $ A \ земя A = A $ и $ \ отр A \ земя А = 0 $, както и че $ A \ oplus A = 0 $, както и опростяване на израза:

$ F (x_1, x_2, x_3, x_4) = (x_1 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 \ отр x_4) + x_2 $

Отново се използва трансформация (1):

$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 \ отр x_4 \ oplus x_2 \ oplus (x_1 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 \ отр x_4) x_2 $

Нека отворена скоба на алгебрични правила:

$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 \ отр x_4 \ oplus x_2 \ oplus x_1 x_2 x_2 \ отр x_3 x_4 \ oplus \ отр x_1 x_2 \ отр x_4 $

Отново използват свойствата на връзка и XOR:

$ F (x_1, x_2, x_3, x_4) = \ отр x_1 \ отр x_4 \ oplus x_2 \ oplus \ отр x_1 x_2 \ отр x_4 $

Замяна на отказ за добавяне на $ 1 $:

$ F (x_1, x_2, x_3, x_4) = (x_1 \ oplus 1) (x_4 \ oplus 1) \ oplus x_2 \ oplus (x_1 \ oplus 1) x_2 (x_4 \ oplus 1) $

$ F (x_1, x_2, x_3, x_4) = x_1 x_4 \ oplus x_1 \ oplus x_4 \ oplus 1 \ oplus x_2 \ oplus x_1 x_2 x_4 \ oplus x_1 x_2 \ oplus x_2 x_4 \ oplus x_2 $

Изхвърли сдвоени условия и получаването на крайната формула:

$ F (x_1, x_2, x_3, x_4) = x_1 x_2 x_4 \ oplus x_1 x_2 \ oplus x_1 x_4 \ oplus x_2 x_4 \ oplus x_1 \ oplus x_4 \ oplus $ 1

метод триъгълник

Триъгълник Метод кодира истина маса в Zhegalkin полином чрез изграждане на триъгълна подкрепа на маса в съответствие със следните правила:

Изграждане на цялостна истина маса, в която редовете са в реда на нарастване на двоични кодове от $ 000 \ dots00 $ 111 до $ \ dots11 $ на.
Построява спомагателната триъгълна масив, където първата колона същата като колона от стойностите в таблицата за истина.
Клетката всяка следваща колона се получава от по модул 2 прибавяне на две клетки от предишното колоната - лице в същия ред и долния ред.
Колони спомагателна маса двоични кодове са номерирани по същия начин, както редовете на таблицата за истина.
Всеки двоичен код е свързан с един от членовете на полином Zhegalkin в зависимост от позицията на кода, в която единиците са. Например, клетка 111 $ $ $ съответства на член на $ ABC, зареден $ 101 $ - членки $ AC $, GSM $ 010 $ - $ легло и $ пишка, кутия $ 000 $ - $ 1 член $ и т.н.
Ако в горния ред на колона е едно, съответният Терминът присъства в полином Zhegalkin.

В действителност, този метод е модификация на метода за изграждане според таблицата на истина, както е описано по-горе. За сравнение, това е по-удобно, че изчисленията заемат малко място и са по-трудно да се направи грешка, но методът на триъгълник изисква по-голям брой операции.

Пример таблица за преобразуване на истината в Zhegalkin полином функция на три променливи $ Р (А, В, С) $ показани на Фиг.

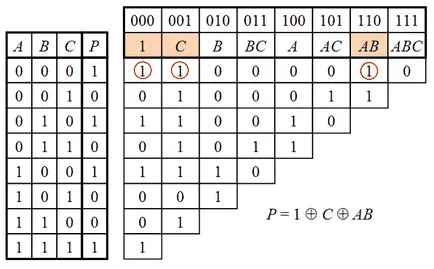
За да се получи формула се използва за изчисляване всеки случай, е необходимо от клетката, в която е записано, да ходи по всички възможни начини от ляво, до $ колона '' P '' $ маса истина, правейки си ходове в ляво и в ляво и надолу, запишете стойностите в сложи край на клетките и ги постави един до друг модул 2.

Така, в първата колона отгоре записва коефициент $ a_0 = P (0,0,0) $,

На второ място - $ a_1 = P (0,0,0) \ oplus P (0,0,1) $,

в третата - $ a_2 = P (0,0,0) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,1,0) = P (0,0 , 0) \ oplus P (0,1,0) $,

$ A_3 = P (0,0,0) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,1,0 ) \ oplus P (0,1,0) \ oplus P (0,1,0) \ oplus P (0,1,1) = \\ = P (0,0,0) \ oplus Р (0,1 , 0) \ oplus P (0,1,0) \ oplus P (0,1,1), $

и така нататък, което означава, че изграждането на полином коефициентите на спомагателни таблицата се изчисляват автоматично.

трансформация Мьобиус

Предвид булева функция $ е: B ^ п \ стрелкаНадясно В, \; \; В =<0; 1>$. Всеки Булева функция може да се представи като полином Zhegalkin, по уникален начин.

Нека $ I = (i_1, I_2 i_n.), \; \; i_k \ в $, и да се въведе система за означаване $ х ^ \ СИМ \ наляво [\ започне х \; \; i_k = 1 януари \; \; i_k = 0 \ край \ прав. $

Тогава Zhegalkin полином може да се запише като: $ е (х) = \ bigoplus \ limits_i \ alpha_i \ cdot x_1 ^ \ cdot x_2 ^ \ cdot $$ \ точки $$ \ cdot x_n ^ $, където $ \ alpha_i \ в <0; 1>$.

$$ набор от коефициенти може да се разглежда като функция от $ \ алфа $ за даден индекс избран $ аз = (i_1, I_2 \ точки i_n) $, т.е. $ \ алфа: аз \ mapsto \ alpha_i $.

Очевидно е, че функция $ е $ могат да бъдат написани както следва: $ е (х) = \ bigoplus \ limits_i \ alpha_i \ cdot [x_1. \; $ Ако $ \; \; i_1] \ cdot [x_2. \; $ Ако $ \; \; I_2] \ cdot $$ \ точки $$ \ cdot [x_n. \; $ Ако $ \; \; i_n] $.

Тук $ рекорд [x_k. \; $ Ако $ \; i_k] $ означава elelement $ x_k $ присъства в съответния срок на полином ако само $ i_k = 1 $. Ако по някаква $ х $, $ аз \ Succ х $ *, тогава срокът ще бъде най-малко един коефициент, равен на нула, а такъв термин за сумата няма да бъде засегната. Следователно е ясно, че $ е (х) = \ bigoplus \ limits_ \ alpha_i $ $ (2) $ Намираме картографиране $ е \ mapsto \ алфа $.

$ * $ $ Аз \ Succ х $ означава, че $ х $ "по-малко от" $ аз $ като последователност от битове

Теорема: Нека функцията $ е $. След функция $ \ alpha_x $ могат да бъдат открити от формулата: $ \ alpha_x = \ bigoplus \ limits_ е (й) $ (3)

Ние доказваме чрез индукция от броя на единиците в вектор $ х $ и за удобство ще означаваме броя на единиците $ тегловни (х) $.

1) База: ако $ х = 0 $, след това очевидно е $ (0) = \ alpha_0 $

2) Да теоремата е вярно за всички суми $ тегловни (х)

Помислете за сумата от $ \ наляво [\ bigoplus \ limits_ \ bigoplus \ limits_ е (к) \ прав] $. Всеки $ е (к) $ елемент се съдържа в него, само ако $ к \ Prec х $, а за фиксиран $ й, х $ елемент $ е (к) $ има точно толкова пъти, колкото има и $ аз $. така, че $ к \ Prec аз \ Prec х $. Лесно е да се види, че такава $ аз $ има точно $ 2 ^ -1 $, т.е. нечетен брой пъти. След $ \ наляво [\ bigoplus \ limits_ \ bigoplus \ limits_ е (й) \ полето] = \ bigoplus \ limits_ е (й) $. Но тогава $ е (х) = \ наляво [\ bigoplus \ limits_ е (й) \ полето] \ oplus \ alpha_x \ Leftrightarrow е (х) \ oplus \ bigoplus \ limits_ е (к) = \ alpha_x \ Leftrightarrow \ alpha_x = \ bigoplus \ limits_ е (й) $. Това е, когато $ тегл (х) = к $ формула притежава, след това за всеки $ х $ работи $ \ alpha_x = \ bigoplus \ limits_ е (й) $.

$ за картографиране е \ стрелкаНадясно \ алфа $ се нарича трансформация Мьобиус.

Човек може да види, че $ (2) $ и $ (3) $ - това е една и съща реализация. Така че, ако ние прилагаме трансформацията Мьобиус до функцията, и след това отново се прилага същата трансформация, за да се получи функция, а след това отново да получи оригиналния функция $ е $. Това е трансформация на Мьобиус обратно към себе си, с други думи, е инволюция.

Вижте също:

Клас $ L $. Теорема на zamknytosti клас $ L $

Неправилни интеграли по безгранична домейн

Свойства на двойни интеграли