Време дисперсия в канала

Начало | За нас | обратна връзка
Връщайки се към ТЯХНОТО (2.3.4). Ако абонатът е в движение, за разпространение на сигнала на характер многопосочно (брой коефициенти за пренос лъчи по сигнал лъчи закъснение) промени. Вследствие на това в канала му също се променя непрекъснато и на случаен принцип. Ние приемаме, че един коефициенти на предаване в (2.3.4) са стационарни случайни комплексни стойности. Също така е естествено да се предположи, че коефициентите на трансфер за различните лъчи са статистически независими. Тези предположения могат да бъдат изразени математически, както следва:
Стойността е средната мощност на излъчване коефициент отделни лъча. Той се счита за да се фиксира, а реализацията на индивидуалния канал може да има различни коефициенти трансмисия. Означаваме коефициент среден трансфер през.
Ако канал генерира много сигнали с различни закъснения, тогава се каже, че има временната дисперсията на сигнала. за характеризиране на време канал дисперсия зависимостта на Р (т) от стойността на предавателната мощност на коефициента на забавяне (мощност забавяне профил). Тази функция може да се нарече спектърът на мощността на забавените сигнали в канала. Тя има падане, а не обикновено плавен характер. Отбележете, че в канал без време дисперсия диапазон на забавяне сигнал мощност Р (т) да се състои от D-импулс при Т = 0 с коефициента на тегло, равно на средната мощност на получения сигнал.
Използване на (2.3.9), ние се изрази функция P (т) чрез своите (2.3.4) като
По дефиниция, средното време на забавяне дисперсията на сигнала канал се изчислява чрез изразяване
Големината на временната дисперсията на сигнала се характеризира със стандартно отклонение от средното закъснение (2.3.11) и се определя както следва:
където - средното закъснение на квадрат равно
Често функция P (т) се нормализира, така че общият коефициент на предавателната мощност е единство, т.е. , Като се има предвид това нормализиране на израза (2.3.11) и (2.3.13) са опростени:
Използването на (2.3.12), ние имаме за времето дисперсията на сигнала
Като пример, разгледа две греди импулсна реакция на канала (2.3.6). В този случай функцията P (т) има формата
Замествайки (02/03/16) в (2.3.11), откриваме, че
Следователно, средното закъснение е по-голяма от нула (време на пристигане на първия сигнал) и по-малко от t2 (второ време на пристигане на сигнала).
Стандартното отклонение на забавянето установено от (2.3.15). В резултат на това ние откриваме, че
Например, на фиг. 2.7 показва дискретни мощност спектър на забавянето на сигнала, който често се използва за моделиране мобилни (клетъчни) комуникационни системи. От тази фигура се вижда, че има шест греди чиито забавяне относително забавяне на първия лъч е 0.31, 0.71, 1.09, 1.73 и 2.51 микросекунди (msek). Ненормализирани изход на тези лъчи са 0, 1, - 9, -10, -15 и -20 db, съответно. Лесно е да се изчисли, че средното закъснение
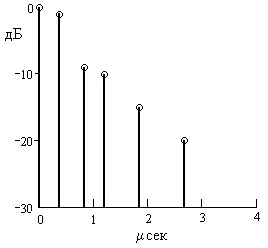
Фиг. 2.7. спектър на мощност на забавянето на канала
Сега помисли предавателната функция (2.3.5), който осигурява коефициент на предавателен канал за хармоничен сигнал с честота е. Коефициентът на предаване е комплексна стойност на случайната защото случаен са съотношения един предаване. Ние считаме, средният коефициент мощност на излъчване на честота F. като се вземат предвид (2.3.9). В резултат на това ние имаме, че
Това означава, че средният коефициент на мощност на излъчване на канала не зависи от честотата и е равна на единство с нормализиране.
От интерес е коефициентът на предаване статистическа връзка канал на двете честоти и F (е -Df), която се определя от функцията на съответствието. Като се има предвид (2.3.5), откриваме, че
Df функция корелация е непрекъсната функция на разликата в честотите и е независим от честотата F. Лесно е да се покаже, че тази функция се трансформира на мощност спектър на Фурие (2.3.10) забавени сигнали, т.е.
За да докаже това, заместваме (2.3.10) в (02.03.21). Получаваме, че
Това съвпада с (02.03.20), което показва, валидността на (03.02.21).
корелация функция определя връзката на домейна канал съгласуваност честота. Тази област се определя polosoychastotnoy последователност канал, който е обратно пропорционална на промяна във времето на сигнала (2.3.15):
Каналът е честотно селективно. ако съгласуваност честотна лента по-малка или съизмерими с ширината на сигнал спектър W. т.е.. Когато са изпълнени условията за обратна връзка. каналът е честотен неселективен или плоска. Този канал, всички честотни компоненти на сигнала, ще бъдат подложени на същото въздействие.
Фиг. 2.8 показва функция модул за канала чиято мощност спектър е представена в закъснения Фиг. 2.7. Тя може да се види, че бандата на половин нивото на честотата на съгласуваността е "0.96 MHz. Продуктът на стандартно отклонение во забавя честотната лента е съгласуваността. това е, от порядъка на единство.
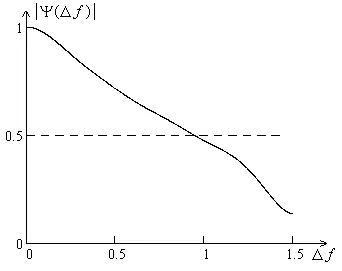
Фиг. 2.8. Модул функция корелация в честотния домейн за мощност спектър канал
който забавяне е показано на фиг. 2.7
Настоящи и бъдещи комуникационни системи като WCDMA, WiMax са предназначени за високоскоростен пренос на данни. За тази избран сигнал с достатъчно широк спектър. Това неизбежно води до факта, че системата ще работи в честотен селективен комуникационен канал. Тези системи трябва да имат специални средства за изравняване на предавателната функция на честотата на канала. Това се постига чрез обучение или пилотни сигнали. Най-много подходящ за тази цел, системата за OFDM комуникация използва за предаване на информация, достатъчно голям брой ортогонални честоти.