Вписан и ограничена цифри

Наречен многоъгълник вписан в изпъкнала крива, и кривата - приблизително многоъгълник описано, ако всички върховете на многоъгълник лежат в крива (Фигура 1.). Наречен полигон окръжност около изпъкнала крива, а крива - вписан многоъгълник, ако всяка от страните му, допирателна към кривата. Ако кривата се отнася за всички линии, по които са страни на многоъгълник, с някои от тях тя се отнася до въпроси, които не са собственост на страните, то се нарича escribed. Кръгът е най-често се разглежда като крива. Например, всеки триъгълник има окръжност кръг, вписан един и три escribed (фиг. 2).

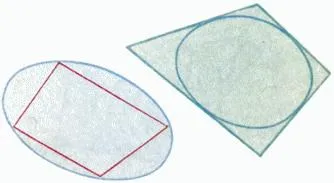
Но не всеки правоъгълник е вписан или окръжности. Окръжност около обиколката на четириъгълник, съществува само ако сумата на противоположни ъгли е равен на 180 °. И така че четиристранни е възможно да се впише в кръг, е необходимо и достатъчно за всеки сумата от дължините на една двойка от срещуположни страни е равна на сумата от дължините на втората двойка страни.

Вписан и ограничена кръгове съществуват във всеки правилен многоъгълник (фиг. 3). Този факт е бил използван в древността да се намери отношението на дължината на окръжността към нейния радиус.

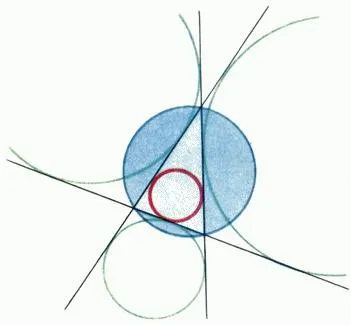
Не е трудно да се открие, че ако равнина е дадена затворена крива и равностранен триъгълник, кръг винаги е възможно да се опише равностранен триъгълник със страни, успоредни на страните на (фиг. 4). По-малко очевидно е твърдението, че около всяка затворена крива може да бъде описан от квадрат.

Вписан и ограничена фигури се разглеждат в пространството.

В този случай, вместо многоъгълник многостен счита, и вместо изпъкнала линия - изпъкнала повърхност, често сфера.

Сферата се нарича окръжност около полиедъра и многостен - вписан в областта, ако всички върховете на полихедронов лежат на една сфера. Сферата се нарича вписан многостен и многостен окръжност около областта, в самолета, ако всички негови аспекти, свързани с обхвата.

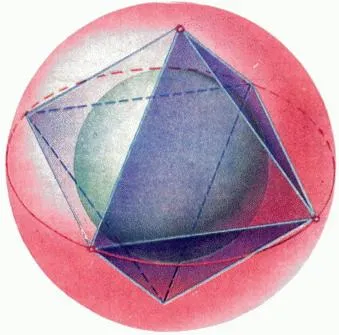
На редовно polyhedra са описани и вписан сфера като върховете на редовен многостен са на еднакво разстояние от центъра (фиг. 5). За други polyhedra има описани и вписан сфера, изисква определени условия. Например, обхватът може да бъде описан за право призма или пирамида, ако кръг около основата може да бъде описан (фиг. 6).

Понякога счита конус вписан в сфера; сфера вписан в конус, цилиндър, и т.н. (Фиг. 7).

На надгробната плоча на Архимед, като завещал учен е изобразен цилиндър вписан с топката, а епитафия да каже за най-голямото откритие на Архимед, че обемите на тези органи се третират като 3: 2. Когато Римската оратор Цицерон и обществен деец, който е живял през I век. Преди новата ера. д. е в Сицилия, той все още виждаше обрасли храсти и тръни паметника с топката и цилиндъра.