умножение на матрици
Матрицата умножение - е един от най-често срещаните операции с матрици. Матрицата, която се получава след размножаване се нарича продукта от матрици.
Продуктът от съм матрица х п матрица да Вп х к матрица Cm х к, така че матрицата елемент С намира в I-ия ред и к та колона, която е ЦНЖ елемент е сума от продуктите от елементи и тият ред на матрицата А, съответстваща на елементи й тата колона на матрицата Б.
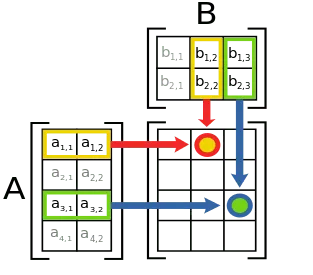
матрица Метод умножение е възможно само, когато броя на колоните на първата матрица е броят на редовете на втората матрица.
например:
Възможно ли е да се размножават матрицата на матрицата?
т = п. Това означава, че се умножи матрицата с данни може да бъде.
Ако матрицата са разменени, след това, с такива матрици, умножение вече не е възможно.
m ≠ п. по този начин, не е възможно да се извърши умножението:
Доста често можете да намерите работа трик, когато ученикът е поканен да се размножават матрици. което очевидно не може да бъде размножаването.
Моля, имайте предвид, че понякога е възможно да се размножават матрици и така и така. Например, за матрицата, и евентуално умножение MN. и умножение NM.
Матрицата умножение.
Действието на умножение на матрици - това не е много сложна работа. Матрицата умножение е по-добре разбрано с конкретни примери, тъй Само решителност може да бъде много объркващо.
Да започнем с един много прост пример:
Трябва ли да се умножава по. На първо място се даде формула за този случай:
- има се наблюдава добра редовност.
След това, по-сложен пример:
Формулата за този случай :.
Matrix резултат умножение:
В резултат се получава така наречената нула матрица.
Важно е да се помни, че не работи тук ", пермутация правило поставя условията", както почти винаги MN ≠ Nm. Поради това, което прави работата на умножение на матрици в никакъв случай не могат да бъдат разменени.
А сега да разгледаме примери за умножение на матрици на третия ред:
Формулата е много подобен на последните;
Размножаване на матрица от редица.
Умножение на матрица от няколко - това е една и съща матрица умножение, с изключение на това, че вместо втората наредба се приема председател. Както можете да предположите, това умножение е много по-лесно да се изпълни.
Пример брой матрица умножение:
Тук всичко е ясно - да се размножават матрица от редица. всеки елемент на матрицата трябва да бъде последователно, умножена по определен брой. В този случай - 3.
Друг полезен пример:
- матрица умножаване с фракционна номер.
Първата стъпка ще ви покаже какво да не правим:
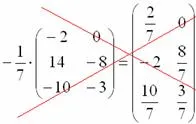
Когато една матрица се умножава по дробно число не трябва да прави фракция в матрицата, тъй като тя е най-вече само усложнява по-нататъшни действия с матрицата, и второ, трудно да се провери решенията на учителя.
И освен това, не е необходимо да се раздели всеки елемент на матрицата при -7:
.
Какво трябва да се направи в този случай - е да се направи по-малко в една матрица:
.
Ако сте имали един пример, когато всички елементи на матрицата ще бъде разделен на 7 без остатък, а след това може да се (и трябва!) Да бъдат споделени.
В този пример, че е възможно и необходимо, за да се размножават всички елементи на матрицата на ½, тъй като всеки елемент на матрицата се дели на две без остатък.
Забележка: висша математика училище концепция за "разделяне" не е теория. Вместо това, фразата "тя е разделена на" винаги може да се каже "това се умножава по една малка част." Това означава, че разделението - това е специален случай на умножение.