Умножение на числа с различни знаци, математика-повторение

Увеличението на броя на отрицателни числа.

Продуктът на две отрицателни числа е положително число. Модул продукт е равна на произведението от броя на модулите на данни.

Тъй като продуктът от положителни числа - това също е положително число, а след това стигна до заключението:

Продуктът на две числа с еднакви знаци е положително число. Модулът на тази цифра е равна на произведението от броя на модулите на данни.

Пример 1. Следвайте размножаването (орално):

Решение. При решаването на всички случаи на употреба се произнесе произведение на две отрицателни числа. По примера на решения а) и б) се прилагат по принцип умножение на десетични 10, 100, 1000 и т.н. При решаването примери в) и г) са общо приложими за умножаване десетичен знак фракция. Ако сте забравили как да го направя - вижте тук!

Решение. Смесени номер в пример б) е обратимо в погрешна фракция. В пример в) второ ниво на продукта фракции заменят две равни части. В пример D) четвърта степен фракция представени като продуктът от четири еднакви множители.

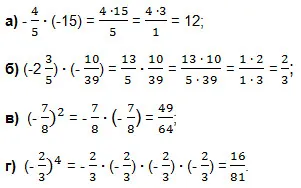
Умножение на числа с различни знаци.

Продуктът на две числа с различни знаци има отрицателно число. Модул продукт е равна на произведението от броя на модулите на данни.

Решение. Прилагането правило се умножи две числа с различни знаци. Умножете мултипликационен модули и преди резултатът ще постави знак "минус".

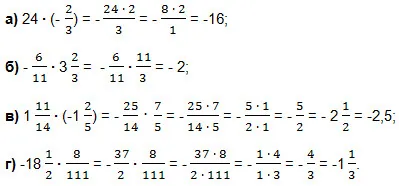
Продуктът на две числа с еднакви знаци е положително число.

Продуктът на две числа с различни знаци има отрицателно число.

Страница 1 от 1 1