Тригонометрични кръг - ELSO дома
На първо място, ние разгледахме отношенията на страните и ъглите на правоъгълен триъгълник. Въпреки това, тригонометрията не свършва дотук. В тригонометрията появява тригонометрични кръг. позволява да се определи позицията на точка на кръга (използван в астрономията) и описват периодичен процес (по физика). Това е благодарение на тази група можем да идентифицират признаци на Синиш, уют, за да видите ясно своите ценности, за решаване на тригонометрия. уравнение - по принцип красота 🙂
Така че, тригонометрични кръг - това е просто една окръжност с радиус 1 с център O за произход (0, 0).
Веднага на въпроса, защо радиуса на кръга е равен на 1? И помни Питагоровата тригонометрични идентичност (син 2 α + защото 2 α = 1) и функцията на обиколката C центриран в точка с координатите (У2 + х 2 = R 2) - изглежда не е вярно 🙂 Веднага виж няколко факти, които радиус R = 1. Също така ние виждаме, че:
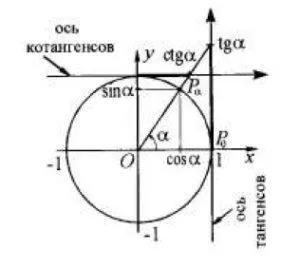
Е, сега погледнем в много кръга. В точката се е усукан периферно Pα (cosα; sinα), и координати са: по оста ОХ х = cosα; от OY у = sinα ос.
И сега отстъплението. В тригонометрията да се използва ъгли в чист вид не винаги е лесно. Например, как да знам грях 4680º и ако защото 444960º. Затова ние въведохме така наречените радиани. Тази стойност също и за измерване на ъгли, но от различна позиция. Съгласихме се, че един радиан - централна ъгъл от дължината на дъгата на която е равна на радиуса на кръга. Според руснака казано 1 rad≈ 57º17 ". Но π рад = 180 °.
Тогава въпросът: ако продължи до стадиона в кръг, вие ще се върнете към началната точка? Разбира се, да. В тригонометрията, същият, както ако въпросът е да се проведе пълен кръг (360º или 2P) тя ще се върне към едно и също място, и най-важното координатите му няма да се променят. Математически, това изглежда така: грях (α + 2πn) = sinα и COS (α + 2πn) = cosα - произволен брой н кръгове около стадиона не Имате ли все още да се върнете към началната точка (ако това 360º или 2p - това е пълен кръг) ,
И сега лесно се счита 1) грях 4680º = грях 26π = грях 0º = 0; 2) COS 444960º = защото 1236π = защото 0 ° = 0.