Точните диференциални уравнения, примери, разтвори

На останали страни на диференциални уравнения на формата понякога са общо диференциали на определени функции. Ако функцията за възстановяване от общия си диференциал, широката интеграл от диференциалното уравнение е намерен. В тази статия, ние описваме метод за възстановяване на функция от общата диференциал, теоретичния материал ще предоставя примери и проблеми с подробни решения.

В лявата част на диференциално уравнение е общата разлика от функция U (х, у) = 0. Ако състоянието.

Тъй като общата разлика от функция ф (х, у) = 0 е, ако състоянието може да се твърди, че. Следователно ,.

От първото уравнение, което имаме. Функцията може да бъде открита с помощта на второто уравнение:

Така ще се намери желаната функция U (х, у) = 0.

Намерете общото решение на диференциално уравнение.

В този пример. Условието е изпълнено, тъй като

Следователно, от лявата страна на оригиналната диференциално уравнение е общата разлика от функция U (х, у) = 0. ни проблем се свежда до намиране на тази функция.

Тъй като не е пълен диференциал на функция U (х, у) = 0. След това. Интегрируеми първо уравнение х и у диференцируема резултат. От друга страна, ние имаме от второто уравнение. Ето защо,

където С - е произволна константа.

По този начин общият интеграл на уравнението е оригинала.

Има и друг начин за намиране на общата разлика от своите функции. Тя се състои в като линията неразделна от фиксирана точка (x0. Y0) до точката с променливи координати (х, у). , В този случай, стойността на интеграла не зависи от пътя на интеграцията. Удобно да се взема като начин за интегриране на прекъснатата линия, връзките на който са успоредни на координатните оси.

Да разгледаме следния пример.

Намерете общото решение на диференциално уравнение.

Проверете състоянието:

По този начин, от лявата страна на диференциално уравнение е общата разлика от функция U (х, у) = 0. намерите тази функция, чрез изчисляване на линия неразделна от точка (1, 1) до (х, у). По пътя на интеграция вземат полигон: първа част наклонени подаване в линия у права = 1 от точка (1, 1) до (х 1). втора част път вземат права линия от точка (х, 1) до (х, у).

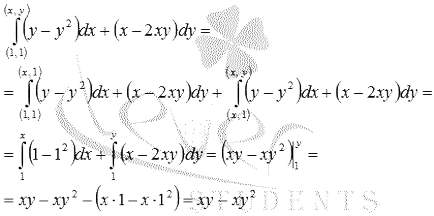
По този начин, общото решение на диференциално уравнение е от формата.