точковите оценки на математическото очакване

ТЕМА: оценки на точката на очакването. за оценяване на промяната Point. Точковата оценка на вероятността на събитията. Крайният резултат на равномерното разпределение на параметрите.

p.1.Tochechnye оценка на очакването.

Да предположим, че функцията за разпределение на случайна променлива ξ зависи от неизвестен параметър θ. P (ξ 0 притежава

По този начин, с увеличаване на размера на извадката увеличава точността на резултата.

Нека х1, х2 ... хп - извадка от населението, съответстваща на случайна променлива ξ с неизвестен средната и известно отклонение Dξ = σ 2. конструкт няколко неизвестни изчисления на параметрите. Ако. нещо, което е помисли за оценка е обективна оценка. Но тъй като стойността не зависи от размера на извадката N, прогнозата не е в съответствие.

Ефективно оценяване на очакването за нормално разпределена случайна променлива е да се оцени

Продължи да оценява neivestnogo очакването на случайна променлива ще използва пробата означава, т. Е.

Има стандартни (редовни) методи за получаване на оценки на неизвестните параметри на разпределението. Най-известните са: метода на моменти. метод на максималната вероятност и метод на най-малките квадрати.

Претенция оценка 2 Spot вариацията.

Σ 2 разсейването на случайна променлива ξ може да предложи следната оценка:

където - пробата да кажа.

Доказано е, че тази оценка е богат, но изместен.

Както последователно обективна оценка на вариацията стойност образуват ispol'uet

Това е обективна оценка на s2 поради нарастващото му използване като оценка на стойността на Dξ.

Имайте предвид, че като Mathcad предлага стойност отклонение оценка вместо е 2. функция Var (х) изчислява стойността

Вземи изключване безпристрастни оценки математическото очакване, Дания Μξ и отклонението на случайната променлива ξ Dξ за дадени стойности за изпълнение на задачи примерни.

Процедурата за прехвърляне

Четене от файл на диска, съдържащ стойността на пробата, или въведете стойността на проба от клавиатурата.

Пример търсене

Вземи изключване безпристрастни оценки математическото очакване, Дания Μξ и отклонението на случайната променлива ξ Dξ от стойности на елементите, уточни следната таблица.

За проби от специфицирани маса тип (дадена стойността на пробата и редица показващи колко пъти е намерена тази стойност в пробата), формулата за богати обективни оценки очакването и дисперсията са от вида:

Фрагмент работен документ оценки Mathcad точкови и изчисления са дадени по-долу.

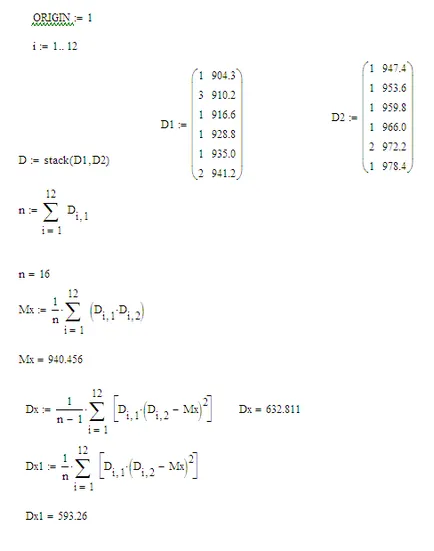
От горните изчисления е ясно, че предубедени оценка дава ниска стойност за оценка дисперсия.

Претенция 3. Точковата оценка на вероятността на събитията

Да предположим, че в някои експерименти събитие на (благоприятен изход на тест-NY) се появява с вероятност р и не настъпва с вероятност р = 1, р. Целта е да се получи оценки на неизвестни р-крак параметър разпределение въз основа на резултатите от случайна поредица от п експерименти. За даден брой опити п брой БАЛ резултати gopriyatnyh М в серия от тестове - случайна променлива с Бернули разпределение. Ние го означаваме с буквата μ.

Ако събитие в поредица от N независими проучвания настъпила

м пъти оценката на предложената стр изчислява по формулата

Изясняване на свойствата на предложената оценка. Поради случайния-маската има Бернули разпределение μ, след Μμ = npiM = М = р. т.е. има обективна оценка.

За теорема валиден тест Бернули Бернули, според която, т.е. Оценка р богати.

Доказано е, че тази оценка е ефективен, като има при равни други условия минимално отклонение.

В Mathcad за моделиране на стойностите на проба от произволни-маски, имащи Бернули разпределение е функция rbinom (FC, η, ρ), който генерира вектор IZK случайни числа, κα-ι zhdoe на които е равен на броя на успех в серия от η независим изпитателен срок, Tany ρ с вероятност за успех във всеки.

Симулиране някои примерни стойности на случайна променлива, като водач-Бернули разпределение с предварително определена стойност на параметъра п. Изчисляват за всяка оценка проба параметър р и сравнение със стойността на данни за. Присъства изчисляване на резултатите в графичен.

Процедурата за прехвърляне

1. Използване на функция rbinom (1, п, р), описва и форма-CHO случайна променлива последователност, като водач-Бернули разпределение с даден р и п за п = 10, 20. Ν, като функция от размера на извадката п.

2. Изчислява за всяка стойност на п дот-вероятност оценка yatnosti стр.

Пример търсене

Пример точка брой обем проба п = 10, 200 20. случайна променлива μ, имащ Бернули разпределение с параметър р = 0.3, по-долу.

Забележка. Тъй като стойността на функцията е векторът, броят на успех в серия от п независими опити с вероятност р успех при всяко изпитване се съдържа в първия компонент на вектора на rbinom (1, п, р). т.е. броят на успеха е равен rbinom (1, п, р). В горния фрагмент к- тия компонент на вектор р съдържа редица успехи в серия от независими проучвания 10k за к = 1,2. 200.

н. 4. Точка оценка на параметрите равномерно разпределение

Позовавайки се на още един пример поучителен. Нека - извадка от населението, съответстваща на ξ съдебната солна стойност, с равномерно разпределение на интервала [0, θ] с неизвестен параметър θ. Нашата задача - да се оцени неизвестен параметър.

Помислете за един от възможните начини за изграждане на необходимата оценка. Ако ξ - случайна променлива с равномерно разпределение, разделяне на интервала [0, θ] ц = ξ. Тъй Mξ стойността оценка известно, Μξ =, тогава за оценка на параметър θ може да оценка

Обективна оценка е очевидна:

Изчисляване на границата на дисперсията D и когато N → ∞, ние проверка на съответствието в оценката:

За други оценки на параметрите θ се обърнат към други статистики. Нека = макс). Намери разпределението на случайна променлива:

След очакването и разсейването на случайна променлива

разпространение са, съответно:

т.е. оценка на богатите, но изместен. Въпреки това, ако вместо = макс) да разгледа = макс), след това. и поради това, платежоспособност и обективна оценка.

В този случай, тъй като

значително по-ефективна оценка

Например, ако п = 97 оценка разпръсна θ ^ 33 Ral малко оценка разпръсна

Последният пример показва още веднъж, че изборът на статистическа оценка на неизвестно разпределение на параметър - важен и nontrivial задача-циален.

В Mathcad за симулация проби случайни стойности на променливите HN с равномерно разпределение на интервала [а, Ь] функция prednazna-Chen runif (FC, о, б), който генерира вектор IZK случайни числа, всеки от които - стойността равномерно разпределени по [а, 6] случайна променлива.

Свързани работи:

т. н. "Точка" финансиране. оценка на риска на риск, свързан с проекта се характеризира с три фактора: на събитието. Поемане на риск; вероятност. matematicheskoeozhidanie. дисперсия. функция на разпределение и плътността на вероятността; определената вероятност.

Вероятности и математическа статистика (5)

вероятност "от ред" намери компонент разпределение. Control. 2) Да се ​​намери matematicheskoeozhidanie и в промените в стойностите на. ;. Нека да matematicheskoeozhidanie и дисперсия. Tochechnuyuotsenku нарича безпристрастен. който matematicheskoeozhidanie грижи.

дисперсионни среди, и неговото стандартно отклонение. Дисперсия. неговата оценка. 4. Проучване и оценка на условията. matematicheskogoozhida-ТА. С други думи, matematicheskoeozhidanie всеки случай равна на абсолютната стойност на това събитие. ум-обвивка на вероятността.

tochechnuyuotsenku проба комплекти за непознатата matematicheskogoozhidaniya. За някои емпирична формула се счита за вариацията S2.

в такива случаи otsenkaveroyatnosteysobyty не е наред - прекалено. Председател на очакванията на хората? Какво е очакването. (Изчакайте - .. равни отклонения в клетките на сложни математически изчисления, например, точка на фигурата се възприема.

Диплома теза >> Финанси

и процедури за оценка на риска в проекта ...................................................................... 47 2.2 Характеристики оценка на изпълнението на проектите. (Например, ликвидност). очакване за увеличаване на първоначалното ниво. вероятността за нежелано събитие (скрипт), и е вероятно.