Теоремата на промяна на кинетичната енергия на механична система - studopediya

форма диференциал. Диференциалът на кинетичната енергия на материалната точка е равна на единица на силата, действаща върху точката,

Integral (крайна) форма. Теорема на кинетичната енергия на материалната точка на промяната: промяната в кинетична енергия на материална точка върху движещ я равна на алгебричната сума от работата на всички активни в този момент на силите на същия ход.

Теоремата на промяна на кинетичната енергия на механична система е формулирана: промяната в кинетична енергия на механична система, както тя се движи от едно състояние в друго, е равна на сумата от работата на всички вътрешни и външни задънена прикрепен към системата, този ход:

В случай на системата непроменен обема на работата на вътрешните сили във всеки ход е нула (), а след това

Закон за запазване на механичната енергия. При шофиране механична система в отговор на сили, които имат потенциал за промяна на кинетичната енергия на системата зависимости определя от:

Сумата на кинетичната и потенциална енергия на системата се нарича общата механична енергия на системата.

По този начин. движението на механична система в стационарна потенциал поле от общата механична енергия на системата по време на движение остава без промяна.

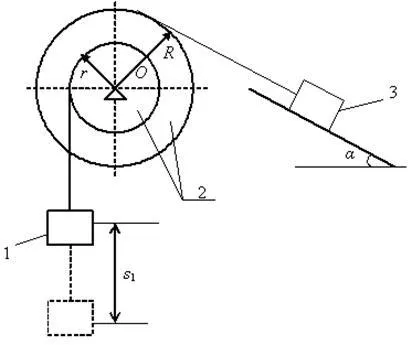
Задача. Механична система под действието на гравитацията в движение от място. Предвид триене плъзгащото тяло 3, пренебрегвайки други сили на съпротивление и маси влакна, предназначени неудължаващ, определяне на скорост и ускорение на тялото 1 в момента, когато те преминават път става равна на S (фиг. 3.70).

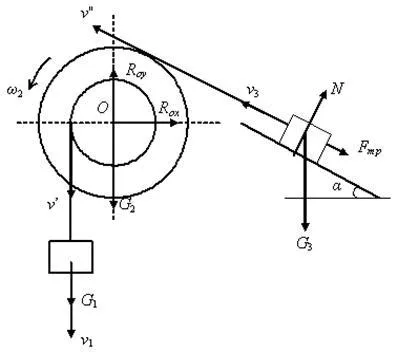
Решение. Механичната система се подлага на активните сили ,. Прилагането на принципа освобождаването от комуникационната система, показват реакция съчленен неподвижна опора 2 и наклонената повърхност грапава. Посока скорости на органите на системата представлява, предвид факта, че тялото 1 се спуска.

Проблем се реши, като се прилагат теоремата за изменение на кинетичната енергия на механична система:

където Т и - кинетичната енергия на системата в началните и крайните позиции; - алгебрични сумата от външни сили, приложени към системата за преместване на системата от началната позиция на финала; - размера на работата на система от вътрешни сили в същия ход.

За разглеждания система, състояща се от твърди тела, свързани с неразтегливи прежди:

След първоначалното състояние на системата е в покой, а след това. Ето защо:

Кинетичната енергия на системата е сумата от кинетичната енергия на телата 1, 2 и 3:

Кинетичната енергия на товара 1, движейки се непрекъснато, е:

Кинетичната енергия на блок 2, се върти около оста Oz. перпендикулярна на равнината на чертежа:

Кинетичната енергия на тялото 3 до нейното постепенно движение:

Изразяването на кинетичната енергия съдържа неизвестни скорости на всички органи на системата. Започнете с определението е необходимо. Отърви се от излишни неизвестни, достигайки ограничаващите уравнения.

уравнения ограничението не е различен от кинематичните отношенията между скоростите и премествания на точки на системата. При формирането на уравненията ограничаващите изразяват всички неизвестен скорост и системите за преместване на органите, които се движат през скоростта и товара 1.

Скоростта на всяка точка на джантата е равна на скоростта на тялото малък радиус 1, както продукта от ъгловата скорост на тялото 2 и радиусът на въртене R на:

Следователно ние изразяват ъгловата скорост на тялото 2:

Ротационната скорост на всяка точка на устройството ръб на голям радиус, от една страна, равна на произведението на ъглова скорост и радиус на въртенето на блока, а другият - скоростта на тялото 3:

Заместването на стойността на ъгловата скорост, получаваме:

Интегриране на първоначално обявените условия (а) и (б), можем да запишем съотношението на точките изместване на системата:

Знаейки скорости в зависимост основните точки на системата, обратно на кинетичната енергия на изразяване и замествайки него уравнение (а) и (б):

Инерционният момент на тялото 2 е равно на:

Замествайки стойностите на масовите организации и инерционния момент на тялото 2, можем да запишем:

Определяне на размера на работата на всички външни сили на системата в даден обем.

Работна сила на тежестта 1

Силата работа е нула, тъй като тези сили са приложени към фиксирана точка.

Работна сила на тежестта 3

Работа нормална реакция на тялото 3 е нула, защото силата е перпендикулярна на посоката на движение

Работа триене при плъзгане

Размерът на работата, извършена от външни сили

Заместването на стойностите на масовите организации, изместването на (а) и числени параметри, можем да запишем:

Сега, според теоремата за изменение на кинетичната енергия на механична система и приравняваме стойности Т

1 скорост тяло, получено от израза (ж)

ускорение на тялото 1 може да се определи чрез диференциране на уравнението от време (г):