Тау за манекени
Записване W (й ω) означава, че W (ите) на предавателната функция е заместен чисто имагинерно число S = й ω. където J = - 1. За всяка честота стойност ω W (й ω) = P + JQ - е Com-
комплексно число с амплитуда от W (й ω) = Р2 + Q 2 и фаза Arg W (й ω) = arctg Q P.
W функцията (й ω) се нарича честота характеристика ниво, тъй като характеризира система изходните сигнали на различни хармонични честоти. В зависимост P (ω) и Q (ω)
(Реални и въображаеми части на W (к ω)) - това е реално и въображаемо честотата характеризира
Функция A (ω) и φ (ω) (за всяка честота, те вземат на реални стойности) HA
свързване, съответно, честотните характеристики на амплитуда и фаза (честота на отговор и фаза отговор). Амплитудна честотна характеристика - фактор печалба на хармоничен сигнал. Ако по някаква честота стойност ω А (ω)> 1, входният сигнал се усилва, ако
А (ω) <1, то вход данной частоты ослабляется.
Формата на честотната няколко основни типа връзки:
1) нискочестотен филтър - преминава нискочестотни сигнали с приблизително еднаква печалба, блокиране висока честота шум и интерференция;
2) високочестотен филтър - предава високочестотни сигнали, блокове нискочестотни сигнали;
3) филтър лентов - позволява само сигнали с честоти в обхвата на ω 1 и ω 2;
4) отхвърляне филтър лента - блокира само сигнали с честоти в обхвата от 1 до ω со 2. Останалите комбинация.
Данните показват амплитуда честотни характеристики на идеални филтри тези четири вида:
6 Това, разбира се, се очаква, че синусоидална система входния сигнал не е "е нищожен", т.е., неговата изходен сигнал не растат без свързан (системата е стабилна).
Ако обектът е нестабилна. След това, когато се прилагат за въвеждане на амплитудата на колебание задължително на изхода ще се увеличи за неопределено време. Въпреки това, на честотната все още може да се определи експериментално. За да направите това, първо трябва да се намери някакъв регулатор, които ще направят устойчив затворена система. След това, във входната R (т) и синусоидален сигнал сравнителен
vayut сигнали х (Т) и у (Т) при входа и изхода на обекта на интерес за нас, определящи за всеки
честотата ω «печалба"
(Съотношението на амплитудите на сигналите х (Т) и у (т)) и преминаването
3.9. Логаритмични честотни характеристики
характеристики честота е доста трудно да се изгради на ръка. През 60-те години, когато разработен класическата теория на управлението, не е имало мощни компютри, така че най-популярните закупени приблизителни методи, с които е възможно да се изработи контролери с ръчни изчисления и конструкции. Един такъв подход се основава на използването на логаритмични честотни характеристики.
Вместо (ω) е предложено използването на логаритмичната амплитуда честота характеристика (LACHH): честота логаритъм графика се нанася по абсцисата (LG со) на и ординатната ос - стойността на L m (ω) = 20lg А (ω). измерва в децибели
(DB). В конструкцията на логаритмичната фаза на честотната характеристика (LFCHH) на абсцисата на логаритъма на честотата като забавено LG ω.
Единицата за конструкция на оста на честота е логаритмична десетилетие - обхвата, в който честотата увеличава 10 пъти (и логаритъм стойност се увеличава). Въпреки LACHH LFCHH и нарича логаритмичната амплитуда честота характеристика на фазата
(Боде парцел) или Боде диаграма.
Логаритмични характеристики имат две полезни свойства:
1) LACHH LFCHH и W 1 за продукта (ите) W 2 (а) се изчислява като LACHH сума и LFCHH отделни единици:
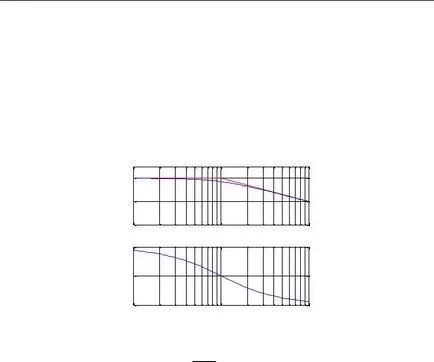
Фигурата показва точното (твърдо синята линия) и асимптотичната (пунктираната червена линия) Боде парцел за първи ред елемент с функция за трансфер
W (а) = Ts + 1 1 за Т = 1 секунда.
Първият асимптота LACHH определя поведението при ниски честоти. има наклон на нула, тъй като връзката принадлежи към класа на позиционни единици имат ненулева постоянно статично печалба, т.е.
Ако W (0) = 0. функцията за трансфер включва фактор и К (к> 0), което съответства
съществува производно за к. В този случай, на склона при ниски честоти LACHH к е 20db / десетилетие.
Ако W (0) = ∞. връзка включва един или повече интегратори. т.е. в знаменателя
има фактор и к. Тогава LACHH наклон при ниски честоти е - к двайсетdb / десетилетие.
Наклон LACHH при високи честоти се определя от разликата в степента на числителя и знаменателя на предавателната функция. Ако числителят е от степен m. а знаменателят - на наш степен. наклона на асимптота е равна на 20 на последната (м - н) db / десетилетие. В нашия пример m - п = 0 - 1 = - 1.
Ето защо, втората асимптота единица определя свойствата с високи честоти е наклонена - 20 db / десетилетие, т.е. на стойност десет години намалява с 20 db (проверка по график!).
4. Типични динамични връзки
Обикновено, системата за контрол се състои от отделни блокове, всеки от които е описан от нисък ред уравнения (по-често - от първа или втора). За да се разбере функционирането на цялата система е желателно да е добре да представлява поведението на отделните му елементи. В допълнение, в изграждането на предавателната функция на Боде парцел от сложна система се разделя на основните фактори
W (и) = W 1 (S) W 2 (а). W N (а)
и по-нататък, като се използва свойствата на Боде парцел построи спецификации за цялата система като LACHH сума и LFCHH индивидуални връзки.
Единици, които имат ограничен ненулева DC печалба на сигнала, т.е. W (0) = к ≠ 0. позиционен наречен. Това означава, че на числителя и знаменателя на прехвърлените
прецизни функции имат ненулеви постоянни условия (постоянните изражение).
Най-простият позиционен блок - идеален (моментално) власт. Неговата предавателната функция W (и) = к. Строго погледнато, това не е динамична връзка, тъй като поради
освобождаване Menen настъпва мигновено, веднага след промяната на вход. Под действието на входен блок стъпка сигнал 1 (т) (или делта функция δ (т)) на изхода ще бъде
усиленият сигнал по време на к, така импулса и преходни характеристики са ниво ч (т) = К (т> 0) и w (т) = к δ (т).
Ако входния усилвател работи на синусоидален сигнал на изхода на той усилва к пъти, без да променя фаза, така че характеристиките на амплитуда и фаза честота не зависят от честотата на входния сигнал:
А (ω) = к. φ (ω) = 0.
4.2. апериодична връзка
Един от най-често срещаните връзки - апериодична. който е описан чрез диференциално уравнение
Асимптотичната LACHH тази единица е оформена от две прави линии, които се пресичат в ъгъл честота ω С, = T 1. При ниски честоти, има нулев наклон (от връзка
позиционен), и в тази област L m ≈ 20lg к.
При високи честоти, LACHH на склона е - 20 db / десетилетие, тъй като степента на знаменателя на предавателната функция е една по-голяма от степента на нейната числител. характеристика фаза варира от 0 до - 90 °. където за чифтосване честота ω с е равна на - 45 °.
Тъй LACHH намалява при висока честота, апериодична елемент потиска висока честота на шума, т.е. филтъра има свойство на ниските честоти.
За сравнение, помислете за нестабилна апериодична елемент. се дава с уравнението
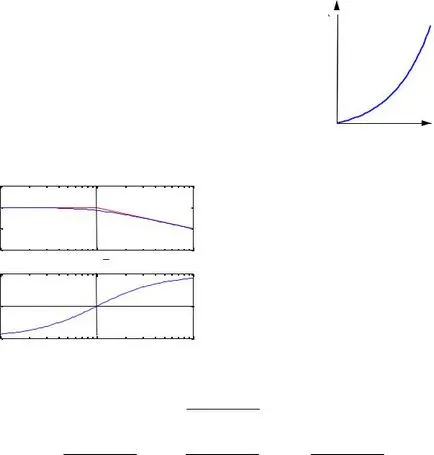
Както можете да видите, като единствената разлика от (39) - Само в знака на лявата страна на час (т) на уравнението (плюс променено на минус). Въпреки това, тя е фундаментална промяна преходното и импулсна реакция:
Обикновено се приема, че времеконстанта Т> 0. Тогава бившия
nents в тези условия е безкрайно увеличават с т.
Ето защо, една връзка, наречена "нестабилна": сам той е в
неустойчиво равновесие, и при най-малкото смущение "е
Интересно е да се сравни характеристиките на честотата на устойчива и
нестабилни връзки с непериодични същите коефициенти и печалбата от време.
От тази графика е ясно, че LACHH neus-
tainable единица точно съвпада с аналогичен LACHH
логически устойчива, но отрицателен Факултативния
zovy измести много повече. устойчивото
апериодична елемент се отнася до минимално
фаза на връзката, т.е. фаза модул
по-малък от фазата на някоя връзка със същото усилва
plitudnoy характеристика. Съответно,
нестабилна връзка - без минимален фаза.
не-минимално фаза Относителните връзки
носени всички връзки, предавателни функции Ko
toryh има нули или полюси в дясната половина
равнина, т.е. положителна veschest-
непълно работно правителствен. За минимално фазови звена на всички нули и полюси на предавателната функция
Те са в лявата половина (има отрицателен реален част). Например, когато
положителен време константи Т 1. Т2 и Т3
връзка с функцията за трансфер
- минималната фаза, и връзките с функции за трансфер
(T 2 е + 1) (Т 3 S - 1)
(T 2 е + 1) (Т 3 S + 1)
(Т 2 е - 1) (Т 3 е - 1)
4.3. вибрационно връзка
Осцилаторна връзка - връзка на втория ред с функция за трансфер на формата
където знаменател е сложните конюгатни корените (т.е., б 1 2 - б 2 4 <0 ). Как извест-
но от теорията на диференциални уравнения, свободното движение на такава система включва хармонични компоненти (синус, косинус) за да се получи на изхода колебание когато входният сигнал.
Лесно е да си представим, предавателната функция на вибрационното ниво под формата
W (и) = Т2 и 2 + 2 T ξ S + 1
(0 <ξ <1). Постоянная времени определяет инерционность объекта,
по-голям е, медта
Нежели излагане изходни промени, когато на входа се променя. По-голямата ξ. толкова по-бързо на вибрациите се заглушават
Когато ξ = 0 в (41) е получен чрез консервативно връзка, която осигурява забавено трептения
изход. Ако ξ ≥ 1, моделът (41) е втори ред апериодична връзка. това е
серийна връзка на две непериодични връзки.
Колебание на кулисата отнася до позиционни връзки, антистатична коефициент
получи равна на W (0) = к.
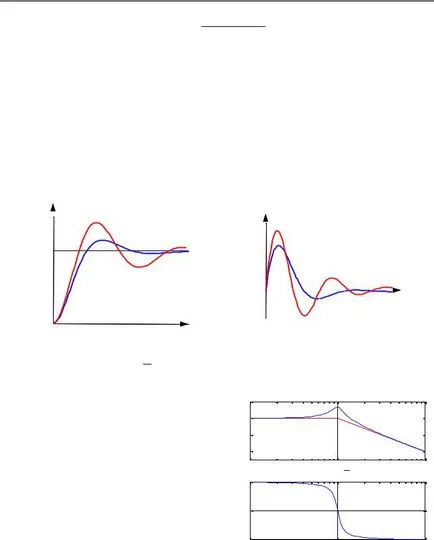
Преход и импулсни характеристики се различават изразени вибрационна,
особено при ниски стойности на затихване на ξ параметър. Следващият две класации синьо
линии съответстват на ξ = 0,5. и червено - ξ = 0,25.
Асимптотичната LACHH тази единица е оформена от две прави линии, които пресичат
на ъгъла честота ω С.
= 1. При ниски честоти, тя има нулев наклон (от линк
позиционен), и в тази област L m ≈ 20lg к.
При високи честоти, по склона е LACHH
тъй като степента на знаменателя РЕ
redatochnoy разполага още две степен на
числител. Фаза характеристика смяна
от 0 до - 180 °. където за чифтосване честота
За стойности на ξ <0,5
наречен "гърбица" в областта на чифтосване
честота, както и височината му се увеличава
намаляване на ξ. Това означава, че ако честотата
тези на входния сигнал, равен на шс. там
резонанс. тоест, честотни звукови вълни съвпадат
Това е естествено честота на трептене на системата.
В случая, когато ограничаване ξ = 0 (консервативен единица) LACHH прекъсване (изготвен
до безкрайност) при честота ω С. в такъв входящ амплитуда на трептене расте без ограничения, и, на практика, се разрушава обект.
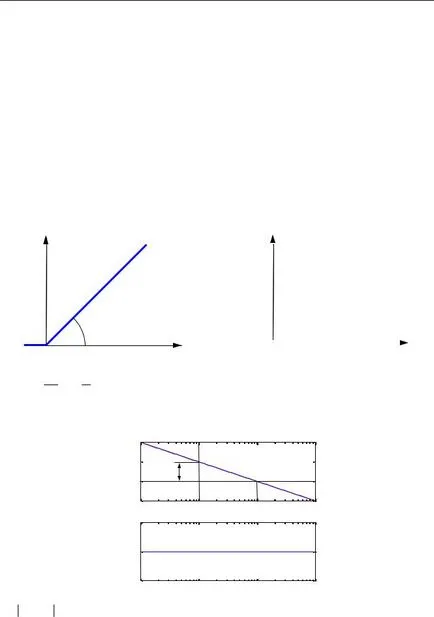
4.4. Интеграторът
Най-простият пример на интегратор - баня, в която се набира водата. Входният сигнал - е потокът на водата през кранчето, изхода на системата - нивото на водата във ваната. При въвеждане се увеличава нивото на водата, системата "натрупва" (интегрира) на входния сигнал.
Интеграторът е описан от уравнението
Очевидно е, че когато сензорът за температура открие незабавно, но след време τ = L / об. където L
- дължината на тръбата (в метри), и V - скорост на въздушния поток (в м / сек). В този случай казваме, че системата е с транспорт закъснение върху стойността на τ (в секунди).
Друг често срещан пример - за изчисляване на забавяне на компютъра. Така го нарича, необходима за изчисляване на нов управляващ сигнал при получаване на всички входящи данни време.
Забавянето в системата просто смени сигнала по оста на времето, без да се променя формата си. Математически, това може да се запише като
Времето за изходна единица изображение сигнал Вие сте
изчислено от теоремата на аргумента изместване за preob-
Y (и) = L
Следователно, предавателната функция единица нетен забавяне равна W τ (и) = д - и τ.