Свойствата на неопределен интеграл - studopediya

Primitive функция и неопределен интеграл

функция F В (х) е примитивна функция на F функция (X) в Х интервал, ако във всяка точка X на интервала
F '(х) = е (х) (т.е., производното на функцията е примитивното).

Например, F (х) = х 3/3 е примитивна функция
е (х) = х 2 от (х 3/3) = X '2.

Имайте предвид, че неговата примитивна уникално определени за всяка функция. Например, за функция е (х) = х 2 примитиви са функции F1 (х) = х 3/3 + 7, F2 (х) = х 3/3 - 10 и, като цяло, всяка функция на формата
F (х) = х 3/3 + C, където С - константа. Това се вижда лесно, като производни на тези функции (производно константа е нула).

По подобен начин, като цяло, ако F (х) - примитивна за F (х), след това, тъй като ((F (х) + С) '= F' (х) = F (х), всички функции на форма F (х ) + C, където С - произволен брой, примитиви са също за F (х).

От изложеното по-горе, не е ясно дали е възможно да се опише във формата на F (х) + C всички примитиви за дадена функция е (х) (може да има и други примитиви, които не могат да бъдат представени като сумата намерено и примитивните константи).

Теорема. Ако F1 (х) и F2 (х) - примитиви за F функция (х), след това съществува номер С, който е F2 на равенство (х) = F1 (х) + С

Като следствие на теоремата Lagrange, ако производното е нула на някои интервал, след това функцията идентично константа на този интервал. Следователно, разликата между тези примитиви ще бъде константа С: F2 (х) - F1 (х) = C Û F2 (х) = F1 (х) + С

От теоремата че експресията е (х) + C са определени за всички възможни примитиви на е (х).

Съвкупността от всички примитивите за F функция (X) в Х интервал се нарича неопределен интеграл на F функция (х) и е означен с
ò е (х) DX, където ò - интегралната знак, е (х) - на подинтегрален, е (х) DX - подинтегрален. По този начин, ò е (х) DX = F (х) + С

Действието на намиране на неопределен интеграл от функция е интеграцията на тази функция.

Това може да бъде доказано, че достатъчно условие за integrability на Х интервал е непрекъснатостта на тази функция в даден интервал (докато за диференцируеми функции за непрекъснатост му е само необходимо, но недостатъчно условие).

Свойствата на неопределен интеграл

Помислете без доказване на основните свойства на неопределен интеграл.

1. производна на неопределен интеграл е равен на подинтегрален, т.е. (ò е (х) DX) `= F (х).

2. Диференциална неопределен неразделна равна на подинтегрален, т.е. г (ò е (х) DX) = F (х) DX.

3. неопределен интеграл на разлика на функция е функция в рамките на постоянен срок, т.е.
ò DF (х) = F (х) + С

Сравнение на свойствата на 2 и 3, може да се каже, че операцията на намиране на неопределен интеграл и диференциални взаимно обратен (г признаци и ò се изключват взаимно в случай на заболяване 3, но с до постоянна).

4. постоянен фактор може да бъде взето извън неразделна знак, т.е.
ò С * е (х) DX = C *ò е (х) DX.

5. интеграл на алгебрични сумата на две функции е сумата от интеграли на тези функции, т.е. ò (F1 (х) + f2 (х)) DX = ò f1 (х) DX + ò f2 (х) DX (този имот е валидна за всеки краен брой събираеми).

Списък ( "маса") основни интеграли

Ние списък интегралите на елементарни функции, които понякога са наричани маса:

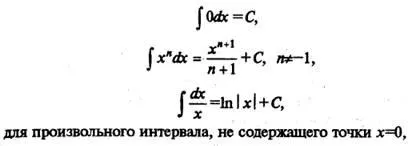
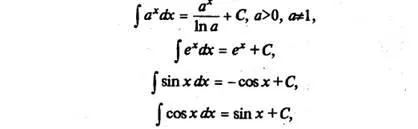
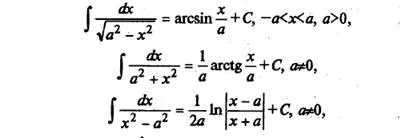
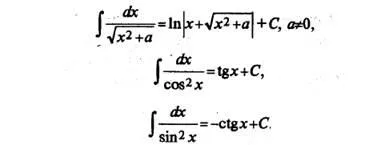
Всеки от горните формули може да се докаже, като производното на дясната ръка (като резултат от функцията подинтегрален се получава).