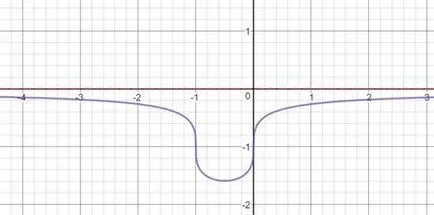
Съвместими система линейни уравнения
матрица уравнение вектор алгебра
Като се има предвид система от линейни уравнения. Докажете го заедно и да разреши по два начина:
а) метод на Cramer;
б) чрез смятане за матрица.
Ние проучва съвместимостта на системата:
Ние използваме Теорема на Кронекер-Капели, за това ние откриваме ранга на разширената матрица на системата и се класира матрица система.
Тук увеличен матрична система на ешалон форма от елементарни трансформации, и определяне на броя на ненулевите редове в матрицата.
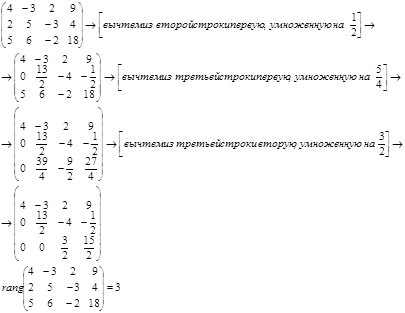
Нека матрична система на ешалон форма от елементарни трансформации, и определяне на броя на ненулевите редове в матрицата.
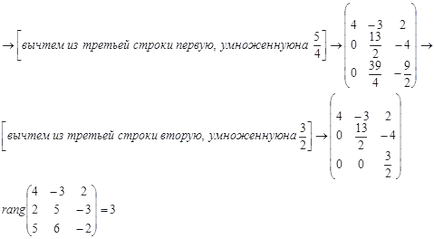
От ранга на системата е равен на ранга на разширената матрица, тогава системата е в съответствие.
Нека да се намери решение на системата, като правило Креймър:
Ние запиша основната матрица на системата и намери своето детерминанта:
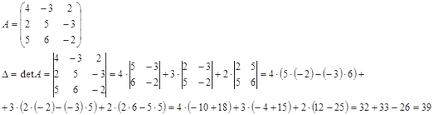
В дефинициите основната система матрица (основната детерминанта) не е нула, системата е съвместно.
Заместник решенията на колоната в първата колона на основната матрица и да намерят своя детерминанта:
Ние замени колона от решения във втората колона на основната матрица и да намерят своя детерминанта:
Заместник вземането на колона в третата колона на основната матрица и да намерят своя детерминанта:
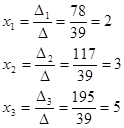
Нека да се намери решение на матрица начин:
Ние намираме обратната матрица. Нека да кофактори:
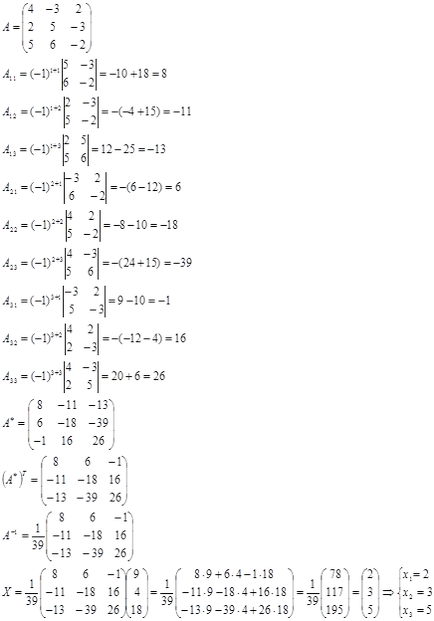
Като се има предвид координати на върховете на пирамида. Средства за векторна алгебра, за да откриете:
2) ъгълът между перките и;
3) в областта на лицето;
4) Обемът на пирамидата;
Намираме А1 А2 ръб дължина с формула
Ъгълът б между краищата А1 А2 А1 А4 и е равен на ъгъла между векторите и. Намираме координатите на тези вектори:
След това ъгълът б определя от съотношението
3) Да се намери вектор продукта
Тогава областта на лицето A1 A2 A3 е
4) Намерете смесения продукт
Тогава обемът на пирамидата:
Докаже, че векторите са линейно независими, и да се намери разширяването на вектора в основата на векторите.
Ние се образува матрицата на координатите на векторите и определя ранг. За да направите това, ние го намали до триъгълна форма.
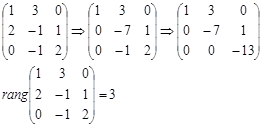
Място векторна система е 3. Векторите са линейно независими и три от тях и защото те са триизмерен, те образуват основа в триизмерното пространство. Всеки вектор пространство може да се разшири във векторите на тази система.
Намираме координатите на разлагане. Ние замени координатите на векторите в последното равенство.
Тъй като векторите са равни, тогава техните координати са равни.
Една система от три линейни уравнения с три неизвестни. реши, че
Разлагането на вектора (6, 12, 1) в тази основа има формата
Като се има предвид трите върха на триъгълника.
а) уравнение страна AB;
б) дължината на страната на слънцето;
в) височината на уравнение понижава от връх А;
г) система на неравенства, които определят триъгълника ABC.
а) страна на уравнението като уравнението AB намери линията, минаваща през две точки:
б) дължината на страната BC намираме разстоянието между текущата В и С:
в) Височина - на линия, минаваща през точка А, перпендикулярна на правата линия, BC. Нека да намерим уравнението на линията BC и неговата посока вектор:
Тогава уравнението на височина:
г) създаване на система за линейни неравенства, които определят един триъгълник. За определяне на знака на неравенството към лявата страна на всяка от двете противоположни страни на уравнения заместващи координатите на върховете, които принадлежат към гарантирана съответната половина самолета.
Заместването на точка C (0, 5) в уравнение страни AB:
Заместването на точка В (18, 8) в AC страна:
Заместването точка А (12, 0) в уравнение страна пр:
Така че, ние напише необходимата система за неравенството:
правило L'Hôpital не е да се намери граници на функции.
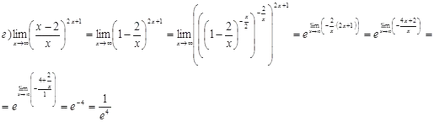
Намери функция точки за пробив, ако те съществуват, функцията за скок във всяка точка на пропастта и изготвите график.
Домейнът на по части - това е обединението на всички нейни компоненти. По този начин,
Очевидно е, че и трите функции са непрекъснати, на подходящи интервали, така че ние ще провери граничните пунктове.
Ние проучи точка х непрекъснатост = -2
- функция се определя в дадена точка
Намираме едностранни ограничения:
Едностранно граници са ограничени и различни, тогава F функция (х) има първа прекъсване за с скок в точката х = -2.
Изчисляват скок прекъсване като разлика между дясното и лявото ограничения:
т.е. графика нарасна до 5 единици.
За да се изследва на непрекъснатостта на точката х = 2.
- функция се определя в дадена точка
Намираме едностранни ограничения:
Едностранно граници са ограничени и различни, тогава F функция (х) има първа прекъсване за с скок в точката х = 2.
Изчисляват скок прекъсване като разлика между дясното и лявото ограничения:
т.е. график върви надолу 4 единици.
Асимптотата там. Има два вида на първо прекъсване при х = -2 със скок равна на 5 и х = 2, с скок равна на -4.
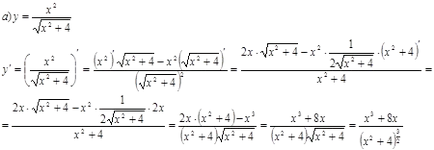
Намерете производните на тези функции.
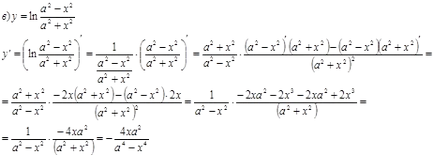
Намерете база радиуса и височината на най-малкия обем на конуса окръжност около радиус R. топка
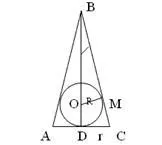
Фигура аксиален разрез през конуса.
ABC - равнобедрен триъгълник AB = BC;
За нас - центъра на вписан в;
М - точката на контакт с периферията на страничната пр;
Г - точката на докосване на триъгълник база okuzhnostyu.
Нека височината на конуса е равен на х, а след това от триъгълника БИС (правоъгълна)
Триъгълниците VSD и ВОМ са подобни в двата ъгъла, след това равенство:
Ние считаме, обемът на конус:
Проверяваме функция V (х) на екстремум:
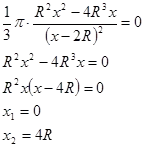
Ние считаме, че една точка х = 4R е минимум точка. Следователно, най-малкия обем на височината на конуса е Н = 4R
Радиус на най-малкия обем на конуса:
Разгледайте методи за диференциални функции смятане и парцел:
1) определяне ОБЛАСТ
2) паритет, нечетен.
Ние се извършва проверка дали някоя от уравнения:
В този случай, функцията ще бъде още по-
В този случай, функцията ще бъде странно
Ето защо, тази функция не е нито дори нито странно. общата форма на функцията.
Ние се заключи, че графиката на функцията не е симетрична по отношение на всяка ос Oy. нито за произхода.
Тази функция не е периодична.
4) функция непрекъснатост.
Цялата област на тази функция е непрекъсната като полином.
5) точките на пресичане на осите
Точките на пресичане с Ox
По този начин, на графиката функция не пресича оста Ox.
Точките на пресичане с оста у
Така пресечната точка е в точка (0, -1)
6) функция по начини завършва домейн.
Краищата на определението на полето са "- # 63" и "+". Ние намираме границите на функцията на
Това показва наличието на хоризонтална асимптота у = 0.
5) критичните точки на функцията, интервалите на монотонност
За да намерите екстремуми на функцията, ние откриваме, производна и да го настроите да е равна на нула, корените на това уравнение са критичните точки.
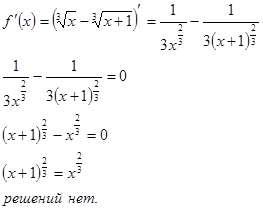
Не екстремум точки.
6) точки на инфлексия, интервали от изпъкналост, вдлъбнатина
Ние считаме, инфлексна точка. За да направите това, вие трябва да намерите втората производна на функцията и тя се равняват на нула. Корените на получената уравнението ще бъдат инфлексната точка за определен графиката на функцията.
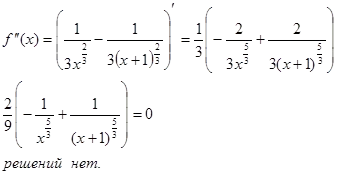
Не инфлексни точки.
7) Скица графиката