Стабилност на линеен сар
Всяка автоматична система за контрол, винаги има различни вътрешни и външни смущения, които могат да нарушат нормалното му функциониране. А правилно проектирани ОСП трябва да работи стабилно при всички сътресения. Определяне на устойчивостта: Устойчивост се разбира способността на системата да се върне с някои точност до състояние на равновесие, след премахване на системата, получен от състояние на равновесие.
За да се изясни значението на понятието стабилност на положението на равновесие на системата, е удобно да се използва следния пример. Нека да има някаква купа, остави на дъното (фиг. 1).
а) стабилна система б) нестабилна система) лимит стабилност
На дъното на чашата (а) в положение на равновесие 1 е тежък топка, която се прилага външна сила може да се отклонява в позиция 2. В даден момент, взети като нула, външната сила се отстранява. Ball, сам на себе си, от позиция 2 пробив и движение по инерция позиция приплъзване 1. След това, достигайки най-високата си позиция, има право на точка 1, топката ще се спусне отново. Като направени няколко осцилиращи движения, топката поради силите на съпротивление спре с определена точност в 1-позиция на равновесие, т.е. определението настъпва равновесие стабилност позиция за краткост обозначен с писмо U. на
В случаите, когато чашата определя с главата надолу (б). Топката отново е в равновесното положение 1 и, ако той не е поставил никакви сили в тази позиция, той ще бъде толкова дълго, колкото е необходимо. Ако някаква външна сила, за да се движи топката в позиция 2, и след това да се премахне тази сила, топката ще бъде изтрит от позиция 1 до безкрайно разстояние, и никога не се върнете към него. Това състояние на равновесие се нарича и е посочено.
В третия случай (с) показва неутрално положение на равновесие или граница стабилност. Ако топката е разположен върху хоризонтална повърхност в 1-ва позиция от външна сила, за да се премести в позиция 2, и след това да се премахне тази сила, топката ще бъде 2-ра позиция, стига да има не се прилага нова външна сила. В случай на неутрално положение на равновесие може да се намери на фиг. 1 и ако има не съществува силите на съпротивление. В този случай, топката ще направи непрекъснати колебания около равновесното положение 1.
Принципът на стабилност на SAR
Нека сега се обърнем към математическата страна на въпроса. Всяка автоматична система за контрол с входен сигнал (външна сила) х Z и изходния сигнал като предавателната функция:
Тя може да се опише чрез линейна диференциално уравнение нехомогенни
н-ия ред с постоянни коефициенти
Решението на този нехомогенни уравнение Z (т,) се състои от обща разтвори zsv (т) е свободен компонент на хомогенна диференциално уравнение
Частни и принудени решения zvyn (т) -vynuzhdennaya компонент, т.е. това, което остава след разпадането на свободната компонент на диференциално уравнение Z (Т) = zsv (т) + zvyn (т).
От дефиницията на стабилност, дадени по-горе, следва, че RAA на резистентност определени в него, след външната сила се елиминира, който довежда ATS на равновесие. С други думи, на стабилността на системата определя zsv (т) преходен процес, т.е. Разтвор на хомогенна диференциално уравнение. Следователно, стабилността на функции на системата са:
Диференциално уравнение (3) съответства на характеристика уравнение (4)
корени, които могат да бъдат или реално (включително нула) или комплекс конюгат (включително чисто въображаема).
Разтворът на диференциално уравнение (3) е известно, че има следната форма (5)
където A, - константи интеграция, определени от параметри на системата и начални условия; пи - корените на характеристика уравнение (4).
Ние считаме, че всички случаи, в самолета
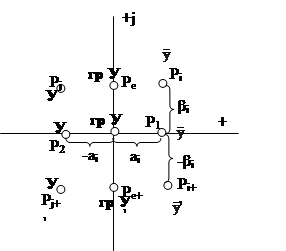
Признак за стабилност на системата
Ако всички корените на характеристика уравнението на ляво (или отрицателен или имат отрицателен реална част), след това системата е стабилна.
Ако поне един от характерните корените на уравнението - дясно система - нестабилна.
Системата се намира на границата на стабилност, ако има корени, разположени на въображаемата ос, освен оставени корени.
Местоположение корен зависи от коефициентите на характеристика уравнението, и следователно, на системни параметри. a0 р п + ... + с = 0.
Ако K2> K1 - корените ще се преместят в дясно.
Ако K3> K2 - може да доведе до нестабилност на системата. Когато става към съпротивлението на корен засенчване намалява.
Колкото по-голяма печалба, толкова по-малко съпротивление (в повечето случаи).
K3> RAG> K2> K1. RAG - параметър при което системата отива в границата за стабилност.
Системата, в която промяната в параметър може да се променя стабилността на системата се нарича структурно стабилна система; в противен случай, когато няма промяна на настройките за нестабилни системи не може да се направи устойчиви, той нарича структурно нестабилна система.
Но корените на уравнението характеристика могат да бъдат изчислени само до 4-то степента и изчисляването на тях е много трудно.
Stodola - изразено състояние, което бе счетено за необходимо, но не достатъчно това.
Stodola състояние: За е необходимо (но не са достатъчни) на всички коефициенти на характеристика уравнението на стабилността на системата са положителни (един знак). Това условие е необходимо и достатъчно за уравненията 1 и 2 порядъци.
Стабилност е предпоставка за правилното функциониране на RAA. Ако отворен цикъл АПК не покрива критична точка (-1, j0), ОСП е стабилен в затворено положение (крива 1 на фиг. I), и, ако споменатият АРС преминава през т. (-1, j0), ОСП е затворен границата за стабилност (крива 2 на фиг. I).
Имайте предвид, че тук по-тясното кривата 1 до критичната точка (-1, j0), толкова по-малко стабилен тя да се затвори ATS. От позицията на АРС Wp (й # 969) на Gaussian равнината, определена от параметрите на системата (печалби, времеви константи и др единици), позицията на криви Wp на (й # 969) близо до точката на привличане може да доведе до погрешни изводи за стабилността ОСП. В действителност, дори и в първоначалното състояние, параметрите на SAR са такива, че съответната крива APC заема позицията 1. Въпреки това, с течение на времето по време на експлоатацията на ATS параметри се променят, и съответстващи на тези променени параметри крива Wp (к # 969;) е станала толкова покрие. (-1, j0), т.е. взема позиция 3. Това означава, че с течение на времето, изчислен като стабилна, ДАБ ще бъде нестабилна.
Тази ситуация няма да възникне, ако ОСП не работи в близост до границата на стабилност. Достатъчно разстояние от него. С други думи, на ОСП трябва да има известна свобода на стабилност, като се гарантира нейната ефективност при различни условия на работа.
Тъй като стабилността на затворената система се оценява чрез критерий Nyquist АРС устройството за на отворен цикъл по отношение на критичната точка, като оценката на ценовата стабилност може да предприеме мерки разстоянието между АРС WP (й # 969) и критична точка (-1, j0). Но позицията на APC Wp (к # 969;) в комплексната равнина за всяка честота стойност # 969; характеризира с фаза и модул. Ето защо въвеждането на концепцията за устойчивост на тези запаси модул (амплитуда) и фаза.
Съгласно стабилност амплитуда марж реализира линеен забавяне на отворен контур точката на АРС с фазата на -180 = 0 критичната точка (1; j0).
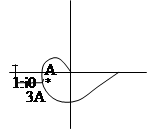
С развитието на храст - за стабилност
амплитуда намалява.
Под границата на стабилност на фазов ъгъл състояние разбира точка АРС модул отворен цикъл = 1 от критичната точка 1; j0.

За стабилни системи ZUF положителни # 947> 0.
За нестабилни системи ZUF отрицателни # 947; 1> 0.
С увеличаване Kusil фаза марж стабилност намалява. За добри системи за качество # 947; = 0 ÷ 30 60 0.