Съхранение в паметта на числа

Целите числа са най-простите числови данни, с които компютърът ви работи. Целите числа се съхраняват по два възможни начина: неподписаните (за положителни числа) и знака (за отрицателни числа). Целите числа в компютъра се съхраняват в фиксирана точка формат.

неподписани числа

За неподписан представителство на всички бита на клетката се разпределят към представителството на номера. Ето защо, ако знаем, че броят е положителен, то е по-изгодно да го третират като неподписан.

Положителни числа заемат PC памет $ 1 $ 2 $ или $ байта.

На $ 1 $ -baytovom формат числа, като стойности от $ 0 до $ $ $ 255.

В $ 2 $ -baytovom формат от $ 0 $ до $ 65 535 $.

Броят на $ 30_ = 0001 \ 1110_2 $ 1 $ $ -baytovom формат:

Броят на $ 30_ = 0001 \ 1110_2 $ 2 байта, формат:

Алгоритъм в областта на компютърните неподписани числа

Неподписани положително число превърне в двоично число система.

Запишете номера в изхвърлянето $ 8 $, така че най-маловажният бит съответства на броя на LSB клетка.

Допълнете номер, ако е необходимо, в ляво с нули до необходимия брой цифри ($ 8 $-ти, $ 16, $ Ti, $ 32 $ ия).

Вземете 8-битово представяне на числото $ 30 $ на.

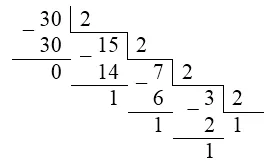
Целите числа

Целите числа (отрицателно), заети в паметта на компютъра $ 1 $, $ 2 $ или $ 4 $ байта, най-значимият (знак) бит дава информация за знака на числото.

Ако номерът е положителен, знаков бит е поставен $ $ "0", ако числото е отрицателно - "1" $ $.

Целите числа в различни формати предприемат съответните стойности:

$ 1 $ -baytovom формат - от $ -128 $ до $ 127 $;

$ 2 $ -baytovom формат - от $ -32768 $ до $ 32767 $;

$ 4 $ -baytovom формат - от -2147483648 $ $ $ до $ 2147483647.

За съхранение на подписаните числа разпределени $ 1 $ знак малко, а останалата част - за цифрите на модула.

Така например, за съхранение на броя на $ 1 до $ -baytovom формат ($ $ 8 бита) $ 1 $ ранг е запазено за знака, а останалите $ 7 $ бита - за броя на модулите.

За съхранение на подписаните числа използва $ 3 $ форма код:

Особено широко използван и обратен допълнителен код, което може значително да улесни основни операции: събиране, изваждане, умножение и деление.

Положителните числа в напред, реверс и допълнителни кодове представляват двоични кодове с цифра $ $ 0 в знаков бит.

Положителните числа имат всички кодове са едни и същи, т.е. напред, назад и допълнителни кодове са равни.

Отрицателните числа в напред, реверс и допълнителни кодове са представени по различен начин.

Директен кодов номер - това е неговата част, преведени на двоична система с променена висок ред малко, в зависимост от знака.

знаков бит е поставена фигура на $ 1 $, а в редиците на цифрови номера - двоична брой модул.

Числата се съхраняват в байтове на компютъра цяло число; $ $ 1, $ 2 $, $ или $ 4 $ 8 $. От размера на паметта, зависи от броя на цифрите на числото. В $ 1 $ байт на $ 8 $, $ $ 2 - $ 16 $ и т.н. Затова е необходимо да се допълни броят на нули на необходимия брой.

Ако цифрите ще заемат в паметта $ 2 $ байта, забележителност ще продължи да бъде най-значителен, а именно: $ -30_ = 1001 \ 1110_2 = 1000 \ 0000 \ 0001 \ $ 1110_2

Обратните код. За операции с отрицателни числа се използва рядко, директен код, така че кодът на връщане е създаден, за да се улесни изпълнението на аритметични алгоритми.

За връщане код се изпълнява Обръщане на всички цифри на двоично число код модула: $ 0 $ се заменя с $ 1 $ и $ 1 $ - до $ 0 $. заустване знак остава непроменен.

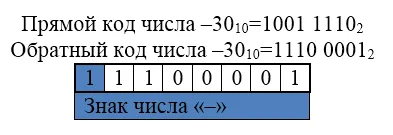
За допълнителна кодов номер на кода на връщане добавя един по-малкия си категория.

Алгоритъм за получаване на отрицателно число на допълнителен код

Отрицателно число въведе пряк код.

Стойността на битова реверсиране на: всички $ 0 $ заменени от $ 1 $, и $ 1 до $ $ $ 0 (с изключение на стойността на знак битова).

Към получената LSB обратен код, за да добавите единица.

Решете контрол по всички предмети. 10 години опит! Цена от 100 рубли. период от 1 ден!

Пишем евтини и точно навреме! Повече от 50 000 доказани професионалисти