Ръководства 866 - Глава 5

където х 1. х 2. .... Xn - някои за оптимизация на параметрите на обекта.

Има два вида оптимизационни задачи - безусловни и условни.

Безусловно проблем оптимизация е да се намери максималната или минимална действителната функция (5.1) на п реалните променливи и определяне на подходящите стойности на аргументите.

Условно оптимизация проблем. или проблем с ограничения - това са, при формулирането на аргументите, на които ограниченията, наложени под формата на равенства и неравенства.

Решението на оптимизационни задачи, в които критерият за оптималност е линейна функция на независимите променливи (т.е. тя съдържа променливите в първа степен) с линейни ограничения върху тях, е предмет на линейното програмиране.

"Програмиране" Думата представлява тук крайната цел на изследването - да се определи оптималния план или оптимална програма, на която от многото възможни варианти на процеса на изпитване се избират на всеки база е най-добрият, най-доброто, опция.

Пример за това е проблем на оптималното разпределение на суровините между различните продукции в най-високата цена.

Нека два вида суровини, изработени от два вида продукти.

Нека: х 1. х 2 - броят на дялове на първия и втория вид, съответно; в 1. С 2 - цена на единица продукция на първия и втория вид, съответно. След това общата стойност на всички продукти ще бъде.

Ние изграждане на система от правоъгълни координати х 1 Ох 2 домейн на възможните решения на проблема (Фиг.11). За да направите това, на мястото на всеки един от неравенствата (5.5) чрез уравнението, ние се изгради съответната гранична линия:

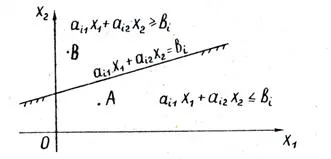
Тази линия разделя равнината на две половини равнини. За координатите х 1. х 2, всяка точка А от една полуравнина следното неравенство:

и координатите на всяка точка в другата половина равнина - обратната неравенството:

Координатите на всяка точка на граничната линия удовлетворяват уравнението:

За да се определи коя страна на гранична линия се намира полуравнина, съответстващ на даден неравенството е достатъчно да "тест" един всяка точка (най-лесният начин да се отбележи О (0, 0)). Ако замяна на неговите координати в лявата част на неравенството е изпълнено, половин обърна към точката за изпитване, ако неравенството не е изпълнено, тогава съответната половин обърна в обратна посока. посока полуравнина показано от люпене на фиг. неравенства

съответства на половин самолет отдясно на ординатата, а по абсцисата.

Фигурата се изгради гранични линии и полу-самолети, които отговарят на всички неравенства.

Като цяло, част (пресичане) на тези половинки равнини ще бъде набор от допустими решения на този проблем.

В изграждането на площта на изпълними решения, в зависимост от конкретния вид на системни ограничения (неравенства) променливи могат да отговарят на един от следните четири случая:

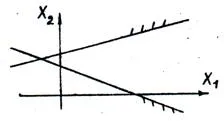
Фиг. 12. Площта на възможни решения е празна, което съответства на системата за несъвместимост на неравенства; няма решение

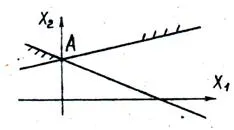
Фиг. 13. Поле допустими решения, представени от една точка А. уникален разтвор, който съответства на системата

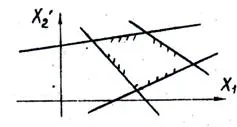
Фиг. 14. Площта на възможни решения ограничават, изобразени като изпъкнал многоъгълник. Един безкраен брой възможни решения

Фиг. 15. Поле допустими решения неограничени във формата на изпъкнала многоъгълна област. Един безкраен брой възможни решения

Графично представяне на обективната функция

фиксирана стойност на R дефинира права линия. и промяна на R - семейството на паралелни прави линии с Р. параметър за всички точки, лежащи на една от линиите, функцията R Прин maet една определена стойност, така че линиите се нарича ниво линии са, за да функционира R.

перпендикулярно на линиите на ниво показва посоката на увеличаване R.

Проблемът за намиране на оптималното решение на системата от неравенството (5.5), за която цел функция R (5.7) достига своя максимум, гео метрично понижено определението в NIJ приемливи разтвори депозитите на точки през които преминават ниво линия, съответстваща на най-голямата стойност schaya-пара- m R

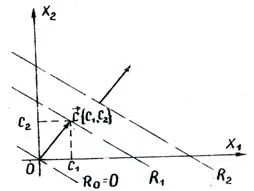
Ако областта на възможните решения е изпъкнал многоъгълник, крайната стойност на R се постига най-малко в един от върховете на многоъгълника-гумите.

Ако се постигне стойност на екстремални на R в два пика, една и съща крайна стойност се достига във всяка точка на отсечката, свързваща тези две връх. В този случай казваме, че проблемът е с оптимална алтернатива.

В случай на неограничен област екстремум на функция R а не съществува или се постига в един от върховете на или алтернативно е оптимално.

Да предположим, че искате да намерите на стойностите на х 1 и х 2. отговарят на системата на неравенството:

и условията на неотрицателност.

за които функцията:

Замяна на всеки от половете неравенства и изграждане на гранични линии:

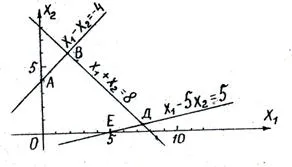
Определяне на половин равнини, съответстващи на тези неравенства, с точка "тест" (0; 0). Предвид nonnegativeness X 1 и X 2 получаваме региона на възможните решения на този проблем под формата на изпъкнал многоъгълник OAVDE.

В областта на възможни решения да намерят оптимални решения, изграждане на вектор градиент

показва посока на увеличаване R.

Оптимално решение съответства на точка Б. Координатите на които могат да бъдат определени графично или чрез решаване на система от две уравнения, съответстващи на гранични линии АВ и VD:

Задачи. Намери позицията на точката на екстремум, а крайната стойност на целевата функция

при определени ограничения.