Резюме информация кодиране - резюмета банкови работи, доклади, курсови работи и дисертации на

2. кодове Класификация

3. Методи за кодове за представяне

3.1 матрично представяне кодове

3.2 Представяне на кодове по код дърво

3.3 Представяне на кодовете, под формата на полиноми

3.4 Геометрични представителни кодове

1. кодиране. Основни понятия и определения

Помислете за основните понятия, свързани с информация за кодиране. За предаване се преобразуват в сигнали в комуникационния канал на комуникация. Символи с който да се създаде съобщение форма основната азбука, всеки символ се характеризира с вероятността за възникването му в изявление. Всяко съобщение съответства еднозначно да сигнал представлява специфична последователност от елементарни дискретни символи наречени кодови думи. Encoding - Това преобразуване съобщение в сигнал, че е преобразуване на съобщения до кодови думи. Кодекс - съответствие между елементите на съобщенията на системата и кодови думи. Енкодер - устройство, което изпълнява кодиране. Dekoder- устройство, което изпълнява обратната операция, т.е. превръщане на кодова дума в съобщението. Азбука - набор от възможни кодови елементи, т.е. елементарни символи (кодови символи) X =, където I = 1, 2. m. Броят на кодови елементи - м се нарича основа. За двоичен XI = т = 2. Крайната последователност на героите от азбуката се нарича кодова дума (кодова дума). Броят на елементите в една кодова дума - п наречения валентен (комбинация дължина). Броят на различните кодови думи (N = Мп) се нарича обем или капацитет на кода.

Ако N0 - броят на източника, а след това N аз N0. Множество от Кодекса на САЩ трябва да обхваща множество състояния на обекта. Пълен еднакво п - цифров код с основата съдържа m N = MN кодови думи. Такъв код се нарича примитивна.

2. кодове Класификация

Кодовете могат да бъдат класифицирани по различни критерии:

1. В основата (броя на символите в азбуката): двоичен (двоично m = 2) и двоичен (m № 2).

2. По дължината на кодови думи (думи):

униформа - ако всички кодови думи имат еднаква дължина;

Неравномерното - ако дължината на кодовата дума, не е константа.

3. Чрез предаване на метод, включващ:

сериен и паралелен;

блокови - данни първо се буферира и след това прехвърлени в двоичен и непрекъснат канал.

4. Шумозащитеност:

прост (примитивен, пълен) - за предаване на информация, използвайки всички възможни кодови думи (без съкращения);

поправителен (радиосмущения потиснати) - за изпращане на съобщения не се използват всички, но само част от (упълномощени) кодови думи.

5. В зависимост от целта и прилагането на следните условни типове код могат да бъдат разграничени:

Вътрешни кодове - кодове, използвани вътре в устройството. Този код машина, и кодове на базата на използване на позиционни цифра системи (двукомпонентни, след десетичната, двоично кодиран десетичната, осмична, шестнадесетичен, и т.н.). Най-често срещаният код в компютъра е двоичен код, което го прави лесно да се приложи в хардуерни устройства за съхранение, обработка и предаване на данни в двоичен код. Тя осигурява висока надеждност на устройството и простота на операциите на данни в двоичен код. Двоични данни, комбинирани в групи от по четири, за да образуват шестнадесетичен код, което е в пълно съгласие с компютърна архитектура, работещи с няколко байт данни (8 бита).

Кодове за обмен на пренос на данни през канали за комуникация. Широко използван в компютъра имам кода ASCII (American Standard Code за информационен обмен). ASCII - е 7-битов код на буквено-цифрова и други знаци. Тъй като компютрите работят с байтове, той е осмият бит се използва за синхронизация или паритет, или код на разпространение. В IBM компютърът използва удължена Двоичното десетичен код за обмен на информация EBCDIC (Extended Binary Coded Decimal Interchange Code).

При кодиране на информация за предаване по комуникационен канал, включително в хардуер пътеки, кодове се използват за максимална скорост на предаване на данни поради елиминиране на компресия и излишък (например, Huffman кодове и Shannon-Fano) и кодове за осигуряване на надеждността на предаване на данни, чрез въвеждане на съкращения в предаваните съобщения (например групи с кодове, Хеминг, циклични и техните варианти).

Кодове за специални приложения - са кодове, предназначени да отговорят на специфичните за пренос и обработка на данни задачи. Примери за такива кодове е цикличен сиво код, който се използва широко в ADCs на ъглови и линейни премествания. Фибоначи кодове се използват за изграждане на високоскоростен ADC и имунитет.

Фокусът на курса се дава кодове за обмен на данни и предаването чрез комуникационни канали.

1) Повишаване на ефективността на преноса на данни, тъй като максималната скорост на данните.

2) Подобряване на имунитета шум по време на предаване на данни.

В съответствие с тези цели кодиране теория, разработена в две основни направления:

1. Теория икономичен (ефективна, оптимално) кодиращата търси кодове позволяващи канали без смущения да се повиши ефективността предаване на информация чрез елиминиране източник съкращения, и най-доброто съвпадение скоростта предаване на данни от капацитета на комуникационния канал.

2. Теорията за корекция на грешката кодиране търси кодове, които повишават надеждността на предаване на данни в шумни канали.

3. Методи за кодове за представяне

В зависимост от прилаганите методи за кодиране, използвайки различни математически модели кодове, най-често се използва код представяне във формата на кодови матрици; код дърво; полиноми; геометрични форми и т.н.

3.1 матрично представяне кодове

Тя се използва за представяне на единна п - цифрени кодове. За примитивен (пълен и еднакво) код матрица съдържа N - колони и 2N - линии, т.е. код използва комбинация от всички. За грешка коригиране (регулиране, откриване и коригиране на грешки), матрицата съдържа N - колони (п = к + т, където к-номер на информация и m - броят на контролни битове) и 2k - редове (където 2k - брой разрешени кодови думи). За по-големи стойности на п и к матрица ще бъде твърде тромави, кодът е писано в съкратен вид. Матрично представяне на кода се използва, например, група от линейни кодове, Hamming кодове и т.н.

3.2 Представяне на кодове по код дърво

Код дърво - свързан граф без цикли. Свързано графика - графика, в която има път свързването на тези върхове всяка двойка на върховете. Графиката се състои от възли (върховете) и ръбове (клонове) свързващи възли, разположени на различни нива. За да се конструира двоичен дърво на еднакво избран връх наречен корена на дървото (източник) и от ръбовете се извършва в следните двата пика, и т.н.

Пример код дърво на пълния код е показана на Фигура 1.

1 0 1 0 1 0 1 0

111 110 101 100 011 010 001 000

Фиг.1. Дърво за пълен двоичен код, когато п = 3

Дърво за корекция на грешката код е изградена въз основа на пълен код дърво чрез изтриване на забранените комбинации на кода. претеглена графика, с краищата на дървото да се посочи вероятността на преходи се използва за дърво неравномерно код. Представителство на кода под формата на код дървото се използва, например, Huffman кодове.

3.3 Представяне на кодовете, под формата на полиноми

Представяне под формата на полиноми кодове на базата на сходство (изоморфизъм) пространство двоичен N - последователности, и пространството на полиноми на степен не по-голямо от п - 1.

Код за произволен брой система с база X може да бъде представен като:

G (х) = с-1 хп-1 + ан-2 + Xn-2. + A1 х + a0 =,

където AI - фигури от корен (двукомпонентни 0 и 1);

х - символично (сляпо) променлива степен, която съответства на двоични цифри chisla-

Например: 1010110 Кодовата дума може да се представи като:

G (х) = 1Chx6 0Chx5 + + + 1Chx4 0Chx3 1Chx2 + + + 1Chx1 0Chx0 = x6 + x4 + х2 + х = 10101

В този случай, работата на кодовете са еквивалентни операции на полиноми. Представяне кодове под формата на полиноми се използва например в циклични кодове.

3.4 Геометрични представителни кодове

Всяка комбинация от п - битов двоичен код може да бъде представен като връх н - триизмерна единица куб, т.е. куб с дължина ръб равно на 1. За две елемент код (п = 2) кодови думи са подредени в квадрат върхове. За кода на три елемента

(N = 3) - по върховете на единица куб (Фигура 2).

Като цяло, н тримерно куба има 2n върха, която отговаря на набор от кодови комбинации 2n.

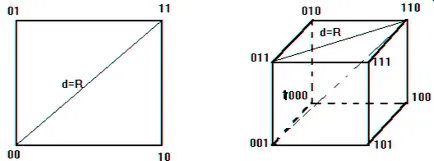
Фиг.2. Геометрични модел на двоичен код

Геометричната интерпретация на код далечината. Код разстояние - минималният брой ръбове, които трябва да бъдат пресечени, за да получите от една кодова дума на другия. Код разстояние характеризира код за корекция на грешката.

Klovsky DD сигнализация теория. -М. Комуникация 1984 година.

Дмитриев VI Приложни Теория на информацията. М. Висше училище по 1989.