Разширяваме определящ фактор по ред или колона, mozgan калкулатор онлайн

За да се изчисли детерминантата на четвърти ред матрици или по-висока може да се разшири детерминанта по ред или колона, или прилага Гаус и води детерминанта с триъгълна форма. Разглеждане на разширяването на детерминанта по ред или колона.

В детерминанта на матрицата се умножава по сумата на определящ елемент ред от техните кофактори:

- разширяване на аз-ти ред.

В детерминанта на елементите на матрицата е равен на сумата от умножена детерминанта колона от техните кофактори:

- разширение в J-ти ред.

За улесняване на разширяването на детерминантата на матрицата обикновено е избран ред / колона, в която / та максималния брой на нула елементи.

Ние считаме, детерминантата на четвъртия матрица ред.

Нека да положи тази детерминанта от колона №3. Направи някои трансформация, която ще улесни по-нататъшни изчисления.

Ние правим нула вместо A43 = 9 елемент. За тази цел реда №4 изважда от съответните елементи на ред №1 умножена по три.
Резултатът е писано в линия №4 всички други линии пренапише непроменени.

Така че ние направихме нули всички елементи, с изключение на a13 = 3 в номера на колоната 3. Сега можете да отидете отвъд и за по-нататъшното разширяване на определящ фактор за тази графа.

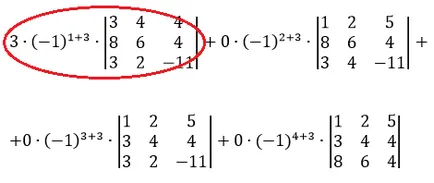
Виждаме, че само терминът №1 не става нула, всички други условия, ще бъдат нули, тъй като те се умножават по нула.
И така, ние трябва да се разшири само един фактор:

Нека да положи тази детерминанта от ред №1. Направи някои трансформация, която ще улесни по-нататъшни изчисления.

Виждаме, че в този ред има две от един и същи номер, така че изважда от колона колона №3 №2. и запишете резултата в колоната №3. от тази стойност на детерминанта не се променя.

След това, ние трябва да се направи нула, вместо a12 = 4 елемента. За тази колона ние №2 елементи умножете по 3 и се изважда от него съответната колона №1 елементи, умножен по 4. Резултатът се изписва в графата №2 всички останали колони пренапише непроменени.

Но в същото време не трябва да забравяме, че ако се умножи по 3 колона №2 е увеличението на детерминанта в 3. Но това, което той не се бе променило, така че е необходимо да го разделим на три.

Ще се намали на числителя и знаменателя с 3.

Така че ние направихме нули всички елементи, с изключение на a11 = 3 в ред номер 1. Сега можете да излиза извън рамките и за по-нататъшното разширяване на определящ фактор за тази линия.

Виждаме, че ни остава една детерминанта на втория ред.

Други материали на

• Намери детерминантата на матрицата онлайн
• Свойства на детерминанта от примерите
• В детерминанта на матрицата от втори ред
• Най-определящ фактор на метода на триъгълник
• Opredelitet метод матрица Sarryusa
• Разширяваме определящ фактор по ред или колона
• Събирането детерминантата на триъгълна форма