разпределение право и основните характеристики на случайните процеси - studopediya
Припомнете си, че всяка изчерпателен характеристика на случайна променлива X - дискретна, непрекъснато или смесен е неговото разпределение функция F = PX
Сега помисли стохастичен процес Х (т). Напречното сечение на случаен процес х (т) за всеки фиксирана стойност на аргумент Т е случайна променлива, която има право разпределение
Тази функция зависи от два аргумента: първо, от стойностите на т. чието напречно сечение се приема; От друга страна, стойността на х. който трябва да бъде по-малко от случайна променлива X (т). Функцията (6.1) се нарича едномерен разпределение право на случаен процес Х (т).
За случайни процеси с непрекъснати състояния, в които всеки раздел е непрекъсната случайна величина, то е възможно да се използва правото на диференциално разпределение.
Ако F (т, х) е частично производно на х
тя се нарича едномерен или едномерен разпределение плътност процес диференциална разпределение право стохастичен X (т).
Ясно е, че едномерна закон за разпределение не е изчерпателно описание на случаен процес. Функция (6.1) характеризира свойствата на който и да е, но само на един участък. То не предоставя информация за съвместното разпределение на две или повече части.
За да се илюстрира този факт, помисли два случаен процес с приблизително същите разпределения във всяка секция (фигура 6.2). Както се вижда на фигурата, тези процеси са напълно различни вероятностни структура. Първо стохастичната процес (а) е с гладка характер, той е имал достатъчно тясна връзка между секциите. За втората (б), тази зависимост избледнява сравнително бързо с нарастване на разстоянието между секциите.
По-пълна характеристика на случаен процес е двуизмерен закон за разпределение
Функция (6.3) дава представа за съвместна дистрибуция на две произволно избрани секции - за Т1 моменти и t2. Но тази функция не е два, а цели четири аргументи, както и неговото използване е свързано с определени трудности в резултат на сложността на експерименталното определяне на законите за двуизмерни разпределение, както и поради своята непохватност в работата си с приложения.
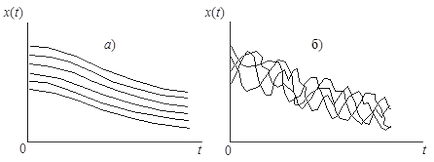
Фигура 6.2. Набор от реализации на две случайни процеси с едни и същи закони едномерни разпространение, но с различна вероятностна структура.
Като цяло, тази характеристика за изчерпателност случаен процес е н тримерно закон разпределение. Въпреки това, има голям клас стохастични процеси (Марков процеси), за които функцията е двуизмерен изчерпателен закон.
На практика, като правило, вместо многомерни закони разпространение се използват основните характеристики на случайни процеси, които описват случаен процес не е напълно но частично.
Както и за случайна променлива дефинирахме математическото очакване, дисперсията, начални и централни моменти, както и за случаен процес, който ще се определят основните характеристики, само случаен процес, тези характеристики не са числа и функции.
Математически очакване на случаен процес X (т) се нарича случайна функция х (т), че за всяка стойност на аргумент Т е математически очакването на случаен процес съответния напречен разрез
където f1 (х т.) - едномерен разпределение плътност на процеса на случаен X (т).
По този начин, очакването на случаен процес представлява някои "средна" функция, около които случаен вариант на метода (фигура 6.3).
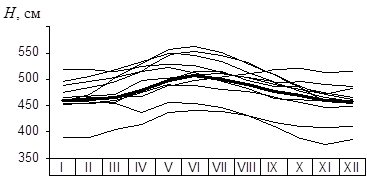
Фигура 6.3. Средни месечни нива на Ладожкото езеро за 1987 - 1988 година (11) и РЕАЛИЗИРАНИ очакване (смела линия).
Ако непознат процес X (т) да приспадне очакване си, ние се центрира случаен процес:
Реализациите центрирани случаен процес представляват отклонения случаен процес X (т) от очакването. Тези отклонения са както положителни, така и отрицателни стойности, а средната стойност е равна на нула:
X (т) на случаен процес се нарича дисперсия неслучайно функция Dx (т), че за всяка стойност на аргумент Т е дисперсията на съответната секция на случаен процес X (т).
Стандартно отклонение на процеса стохастичен X (т) се нарича случайна функция SX (т), е равен на корен квадратен от дисперсията на случаен процес:
измерение функция SX (т) е равен на размера на стохастичен процес Х (т).
Очакване и отклонения са важни, но не са изчерпателни характеристики на случаен процес, както е определено от само едномерна закон за разпределение и не позволяват да се вземе предвид естеството на връзката между отделните участъци. За да се отчете тази връзка при използване на корелация функция на случаен процес.
Съотношение (или ковариация) функция на случаен процес X (т) се нарича случайна функция Kx (т, т), че на всяка двойка аргумент стойности Т и Т 'е равна на съответната сечения ковариация X (т) и X (т):
Имайте предвид две важни свойства на корелационната функция:
1. равни аргументи (Т = т ') е корелация функция на отклонението на случаен процес. В действителност,
2. корелационната функция Kx (т, т ') е симетрична по отношение на неговите аргументи:
Заедно с корелационната функция с помощта на функцията за нормализирана корелация.
Нормализирано съотношение функция RX (т, т ') на случаен процес Х (т) е функция получава чрез разделяне на корелация функция на продукта на стандартните отклонения SX (т), SX (т):
Свойствата на функцията нормализирано съотношение:
1. В случай на равенство аргументи тон и нормализира функцията на корелация т 'е равен на една:
2. нормализирано съотношение функция RX (Т, Т ") е симетрична по отношение на неговите аргументи:
3. нормализирано съотношение функцията на модула, да не надвишава единица:
Досега говорихме за скаларна случаен процес, но има вектор случайни процеси, в които като съставки могат да включват две или Боле случаен процес.
Например, като вектор случаен процес може да се разглежда като промяна в прекарва време в няколко измервателни уреди.
За да се опише вектора на случайни процеси е необходимо да се знае, очакването и корелационната функция за всяка точка на процеса, включени в вектор случаен процес като компонент. Освен това е необходимо да има характеристика, която отразява връзката между отделните компоненти на вектора на случаен процес. Като такава характеристика се използва функцията за кръстосана корелация.
Функцията на взаимна корелация, Ri, J (т, т ') на две произволни процеси Xi (т) и Xj (т ") се нарича произволна функция на два аргумента Т и Т'. при което всяка двойка от стойности на Т и Т 'е ковариация на двете секции на случаен процеси Xi (т) и Xj (т):
Ние списък на основните свойства на функцията на взаимна корелация:
1. Функцията на взаимна корелация, Ri, J (т, т) обикновено не е симетрична в свои аргументи:
2. Когато и двата показателя се променят местата и аргументи кръст функция корелация не се променя:
3. В случай на равенство I = индекса й взаимна корелация функция е корелация функция на случаен процес Xi (т):
Случайни процеси Xi (т) и Xj (т) се наричат несвързани помежду си, ако тяхната взаимна корелация функция Ri, J (т, т), равно на нула за всички стойности на Т и Т 'при условие, че.