Размити номер 4
4.1 Концепцията за размита номер
Размити брой - това размити променливи върху реалната ос, с други думи, размита номерът е определен като размита комплект

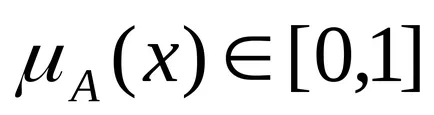
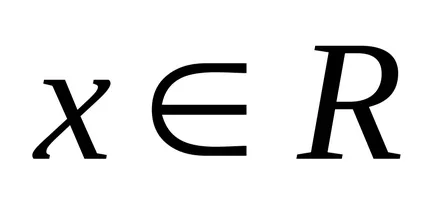
Размити брой се нарича нормално. ако изпъкнала. ако по някаква
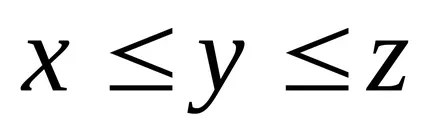
.
много


.
подмножество
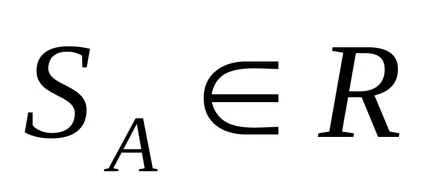

.
Унимодално размита номер. ако условието
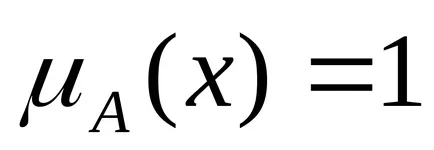
Изпъкналите размито число се нарича размита нула, ако
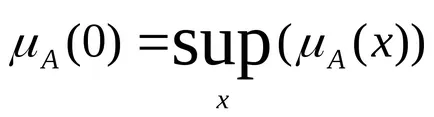
Размити брой е положителна. ако

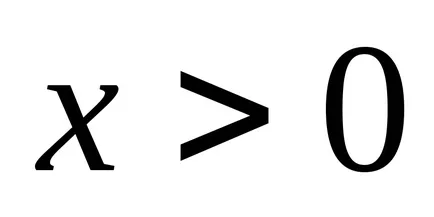

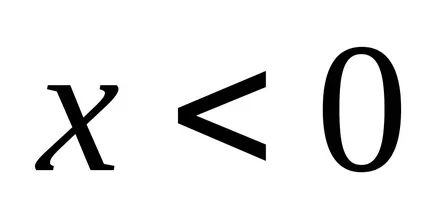
4.2 Операции на размита номера
Разширен операции двоично аритметично (. Освен това, умножение и т.н.) за размита номера са определени чрез подходящи операции за изчистване номера използват обобщение на принципа, както следва:
Използвайте така определените алгебрични операции на размитите числа е непрактично поради големия размер на изчисление. Така че това често се използва в представителството на размитите числа
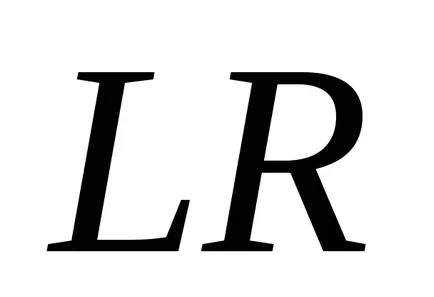
Размити номер в
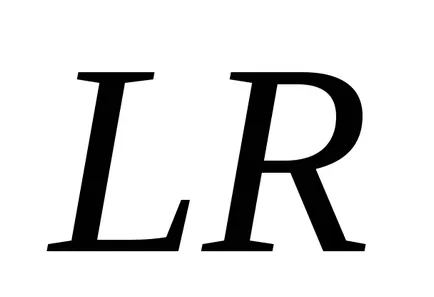
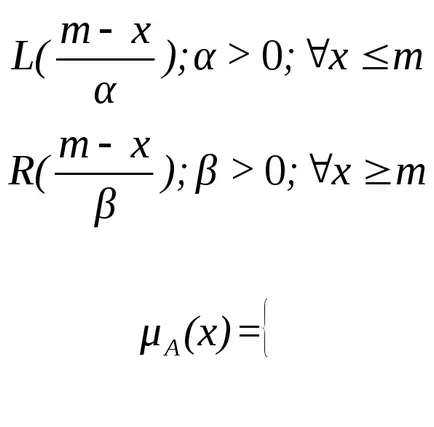
където
,
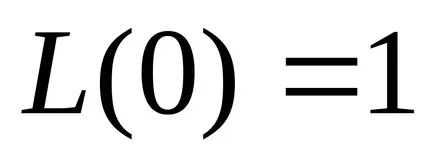
функция
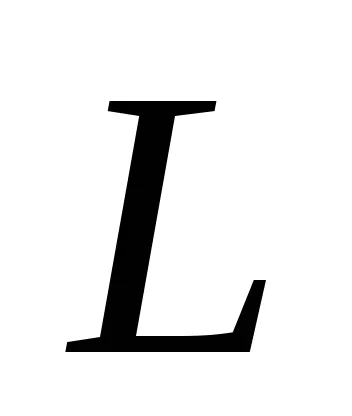
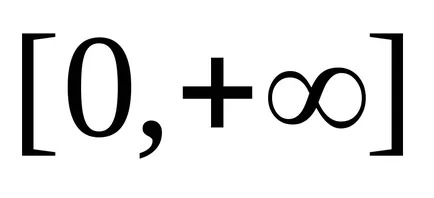
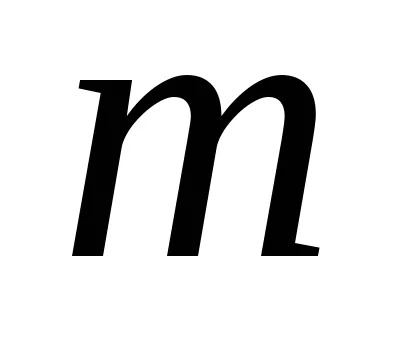





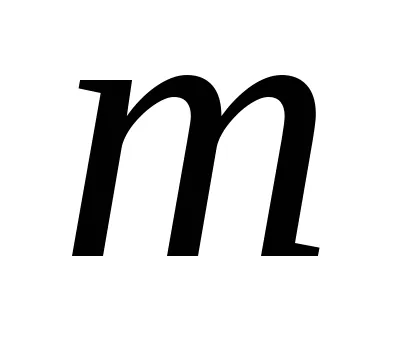
По този начин, размита номер
на практика
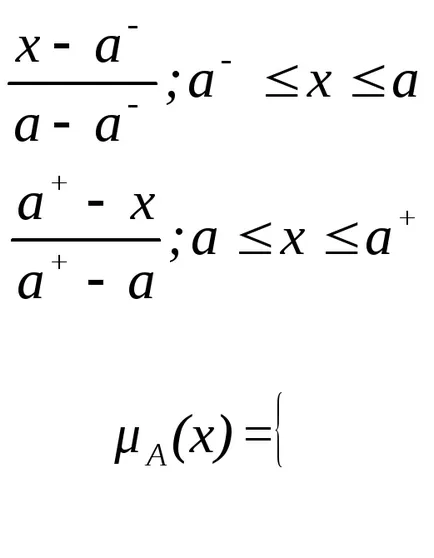
Освен това пролиферацията на трапецовидни форма функции членство, които имат формата
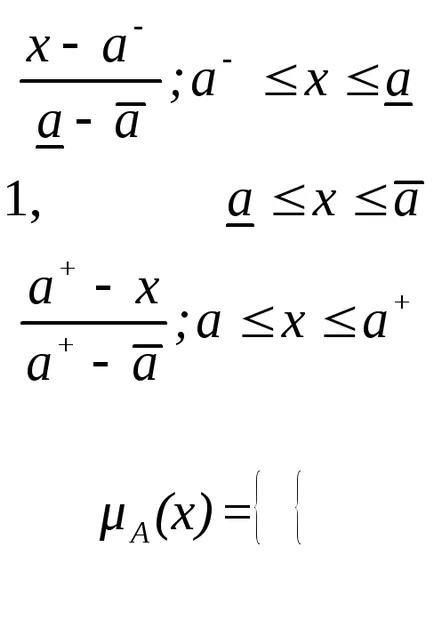
Решаването на проблемите на математическо моделиране на сложни системи, използващи размити множества, изискваща голям обем на операциите на различни видове езикови и други неясни променливи. За удобство на операциите, а също и за IO и съхранение, е желателно да работят функциите на стандартните аксесоари тип.
За съжаление, дори и с намаляването на размитите числа до концепцията за брой триъгълници, остават нерешени проблеми на обратното и да се обърне елементи и разпределителни имота. Друг съществен недостатък на този подход. Blur продукт зависи не само от фактори, размазване, но също така и на мястото, което заемат данни размити числа върху реалната ос. Например, нека
А = (1, 2, 3), В = (2, 3, 4), след това AB = (2, 6, 12)
и С = (99, 100, 101), Е = (100, 101, 102),
ако СЕ = (9 900 10 100, 10 302).
От този пример следва, че на Съвета на Европа по-неясно от AB.
Размити множества, които трябва да бъдат използвани в повечето задачи обикновено са унимодално и нормални. Едно от възможните методи сближаване на размити множества е еднакво приближение, използвайки