Рационални корените на полином с цели коефициенти

Въпросът за намиране е (х) полином рационални корени

Q [X] (с рационални коефициенти) намалява намиране корените на рационални полиноми к ∙ е (х)Z [X] (с цели коефициенти). Тук, номер К е най-малкото общо кратно на знаменателите на коефициентите на полинома.

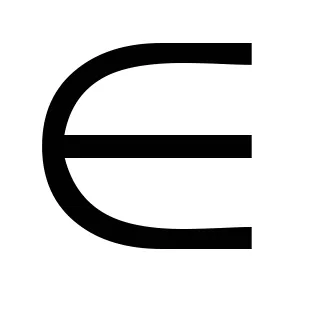
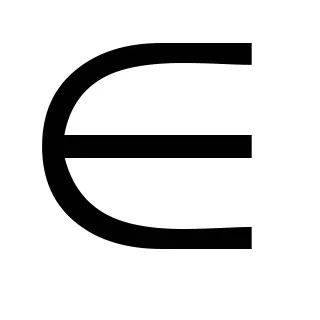
Необходими, но не достатъчни условия за съществуването на рационални корени на полином с цели коефициенти, дадени от следната теорема.

Теорема 6.1 (на рационалните корените на полином с цели коефициенти) .Ако

mnogochlenaf рационален корен (х) = anxn ++ ... + a1x + a0stselymikoeffitsientami, където (р, р) = 1, числител константа a0 drobipyavlyaetsya делител и делител znamenatelqyavlyaetsya водещ коефициент a0.

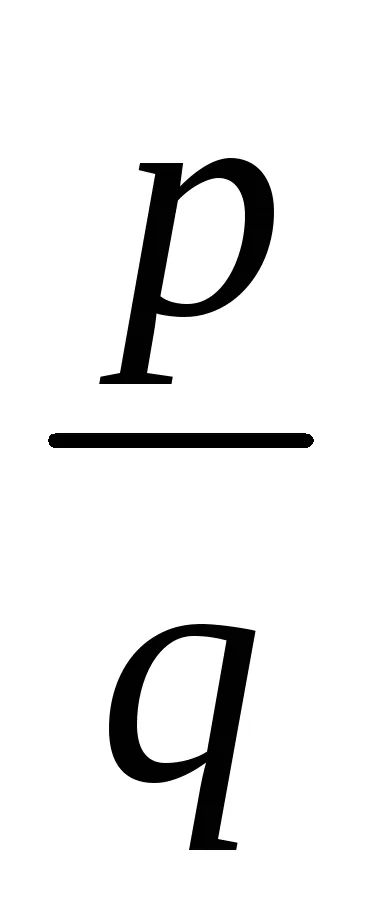
теорема 6.2.Esli

Q (където (стр. Q) = 1) е рационално mnogochlenaf корен (х) с цели коефициенти,са цели числа.

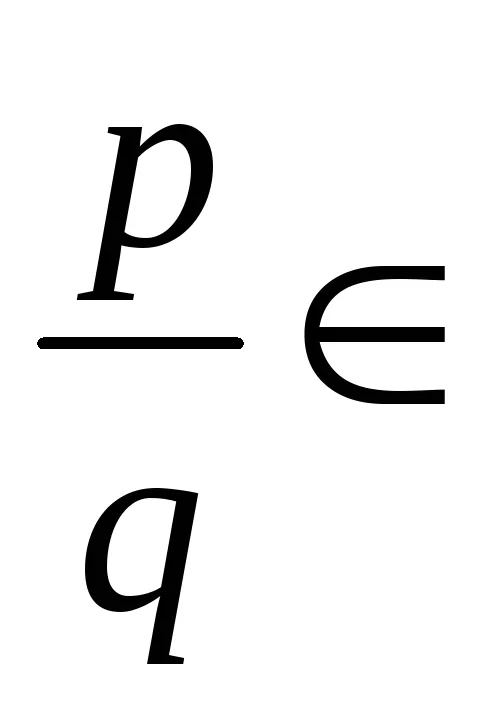
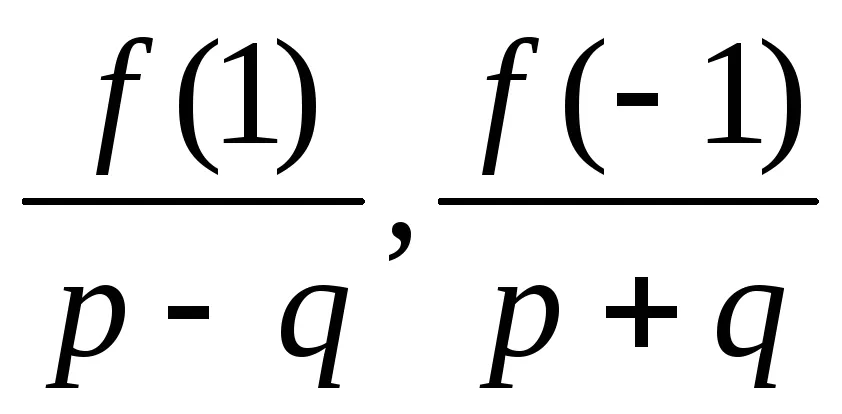
Пример. Намери всички рационални корени на полинома

1. Чрез Теорема 6.1: ако

- рационален корен на полином F (х), (където (р, р) = 1), след това a0 = 1 р, с = 6 р. Затова р 1>, р, средства

.

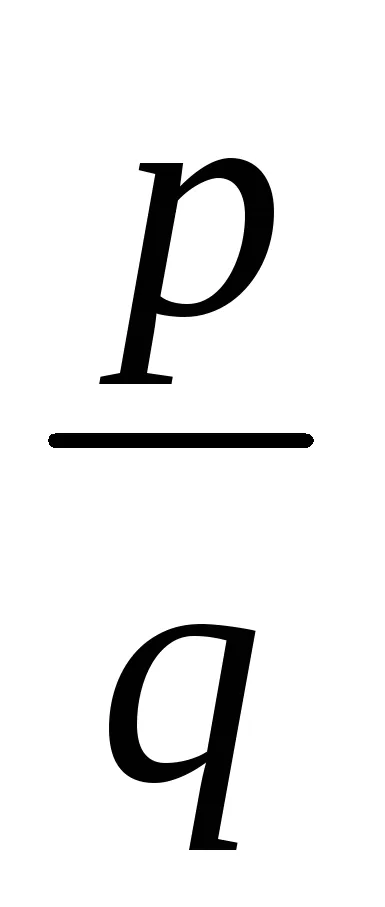
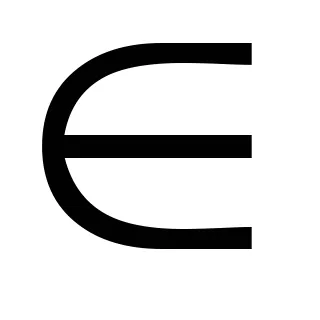
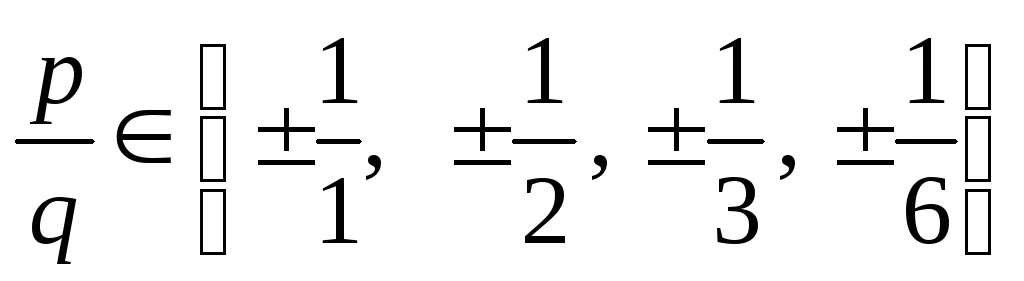
2. Известно е, че (Следствие 5.3), номер А е корен на полином F (х), ако и само ако е (х) е разделен от (х - а).

Следователно, за да се провери дали числата 1 и -1 корените на полином F (X) могат да използват схема Horner:

Получено: Q (

) = 0, т.е.- korenq (х), и следователно, - korenf (х). По този начин, полином F (х) има две рационален корен: и.

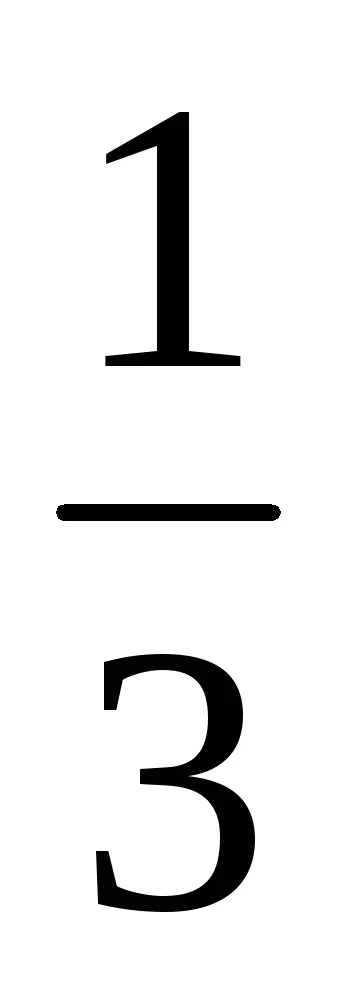
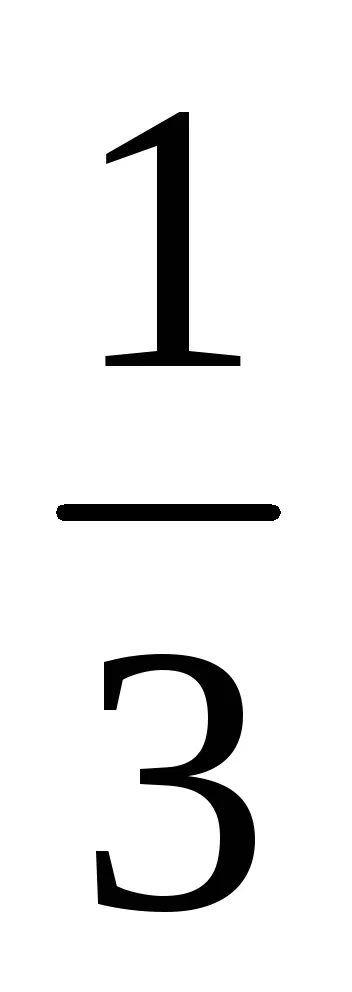
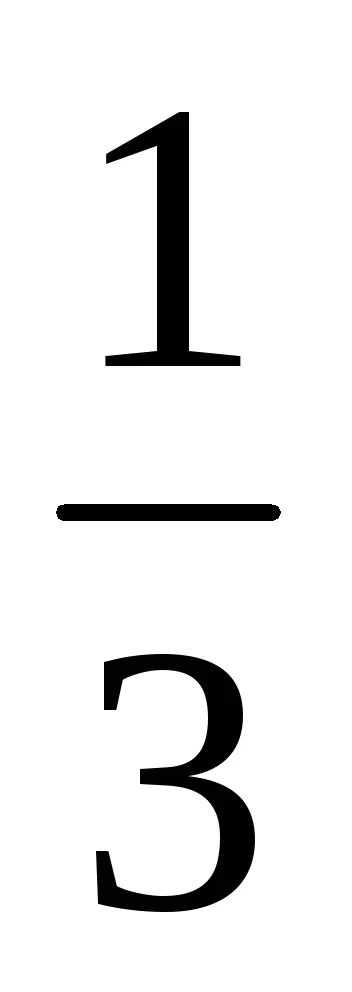
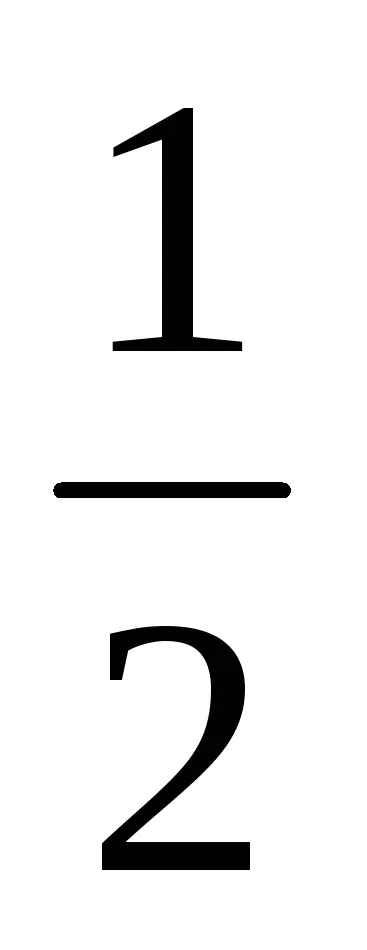
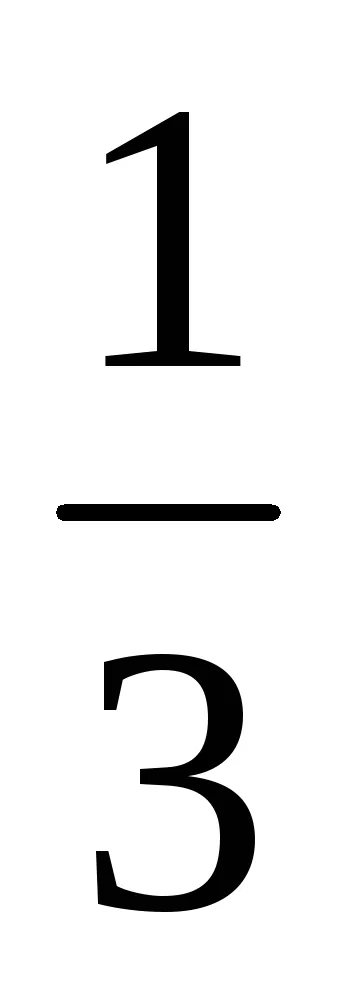
Освобождаване от алгебрични ирационалност в знаменателя на фракцията

Курсът на училище за решаване на някои видове проблеми за освобождаването на ирационалността в знаменателя на фракцията е достатъчно да се размножават на числителя и знаменателя на броя конюгат знаменател.

Тук, в знаменателя с формула се активира Инициали умножение (разликата от квадратите), който позволява свободно на ирационалност в знаменател.

2. Да се ​​отървем от ирационалност в знаменателя на фракцията

т =

. Експресия - част квадратен от разликата на номера = и б = 1. Използване формула Инициали умножение a3-b3 = (А + В) · (а2-аб + b2), може да се определи фактор m = (А + В) = + 1, която трябва да умножим и знаменателят drobit. да се отърве от ирационалност в знаменателя на фракция тон. По този начин,

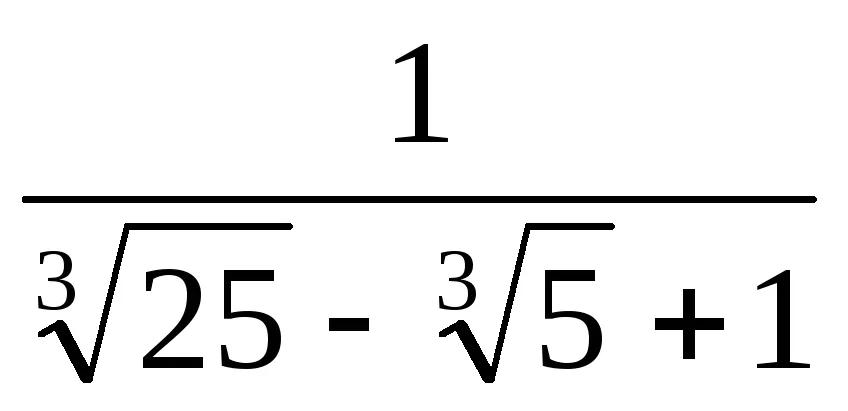
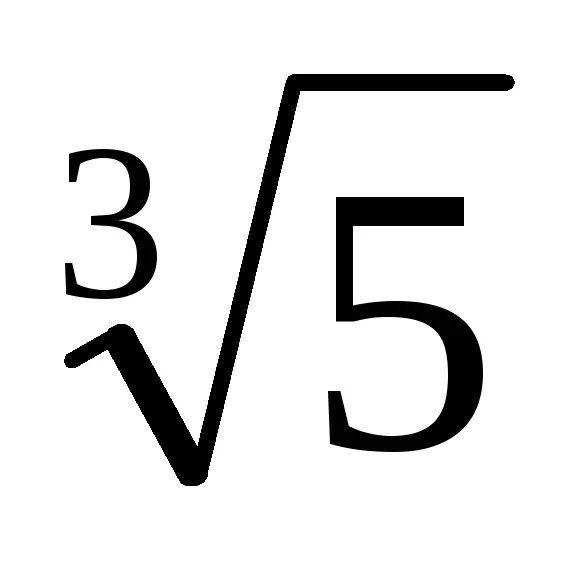
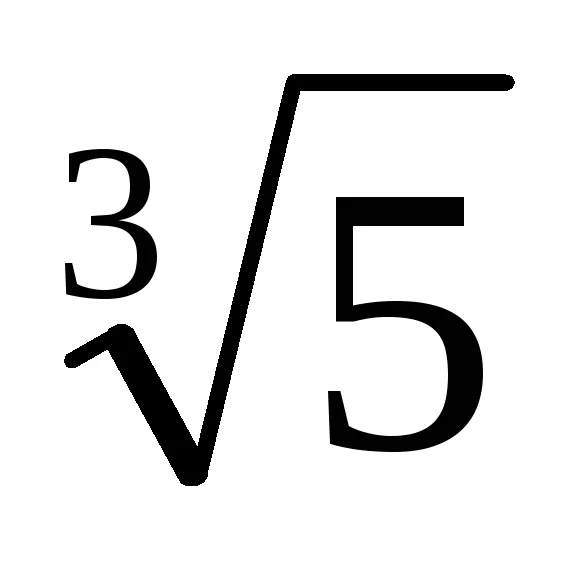
В случаите, когато формулите на съкратена умножение не работи, можете да използвате други техники. По-долу сме се формулира теорема, доказателство за което, по-специално, тя позволява на алгоритъма за намиране освобождаване от ирационалността в знаменателя на фракцията в по-сложни ситуации.

Определение 6.1. Z на брой се нарича алгебрични над polemF. ако съществува полином е (х)

F [X], чийто корен е Z. в противен случай номер Z се нарича трансцендентално над polemF.

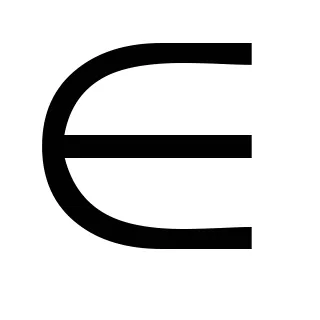
Определяне 6.2.Stepenyu алгебрични над polemFchislaz нарича степен който не може да бъде принуден полином над полето F р (х)

F [X], чийто корен е номер Z.

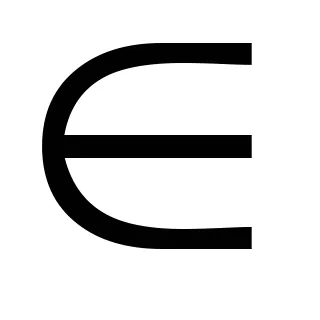
Пример. Ние показваме, че Z = брой

Това е алгебрични над polemQ и намери своето ниво.

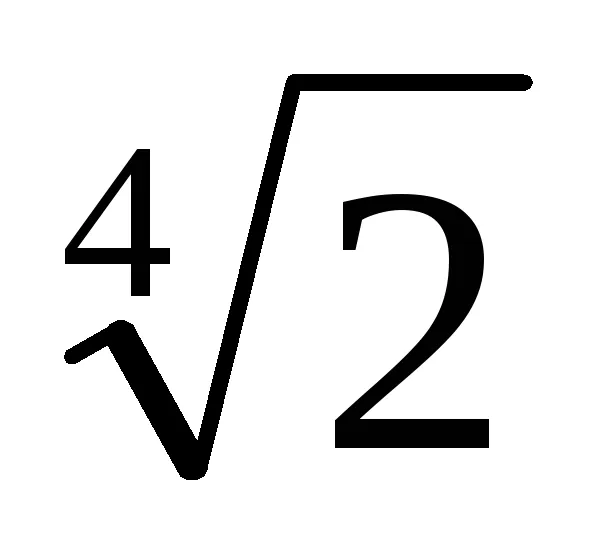
Ние намери несводима полином над поле Q р (х), в основата на които е х =

. Повишаване на двете страни ravenstvax = четвъртата власт, или poluchimh4 X4- = 2 2 = 0. По този начин, р (х) = X4- 2, и Z е равна на мощност на DegP (х) = 4.

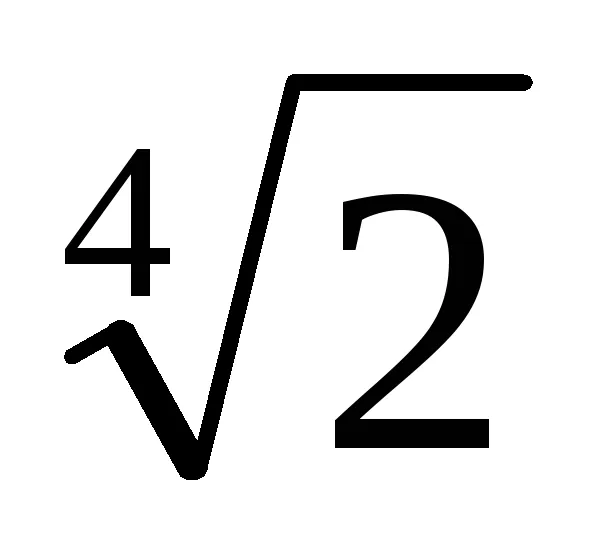
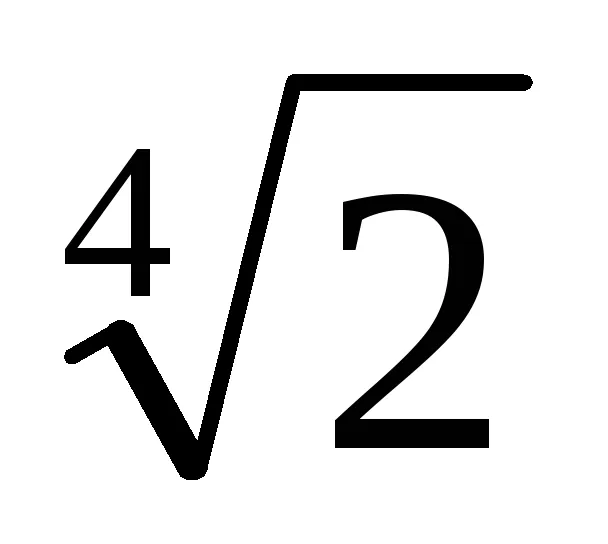
Теорема 6.3 (освобождаването на алгебрични ирационалност в знаменателя) .Pustz- алгебрични брой над polemFstepenin. Експресия vidat =

,където F (х), (X)F [X], (Z)0

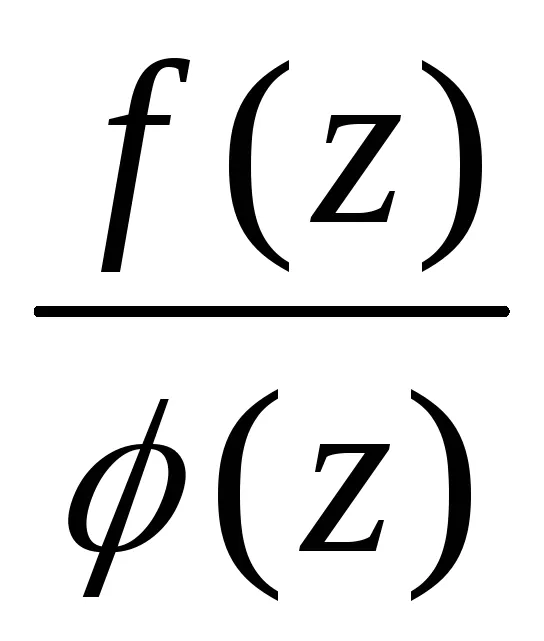
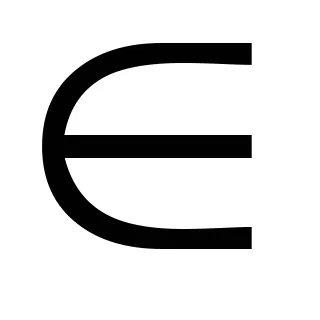
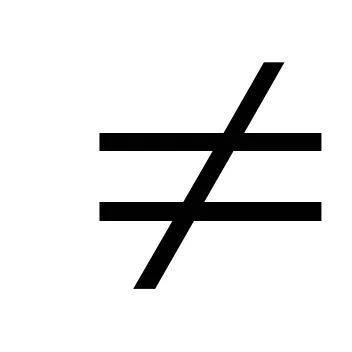
Тя може да бъде еднозначно представени в следния вид:

т = CN-1zn-1 + CN-2zn-2 + ... + c1z + c0. CI

F.

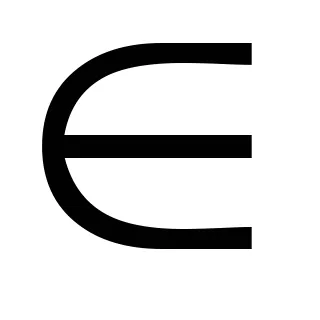
Освобождаването на ирационалност алгоритъм ще демонстрира специфичен пример в знаменател.

Пример. Безплатно от ирационалността в знаменателя:

1. знаменател на малка е стойността на полином

(X) = х 2 - х 1 х = . В предишния пример показва, че- polemQ над алгебрични брой на степен 4, тъй като тя е корен на несводима полином над Q р (х) = 2 X4-.

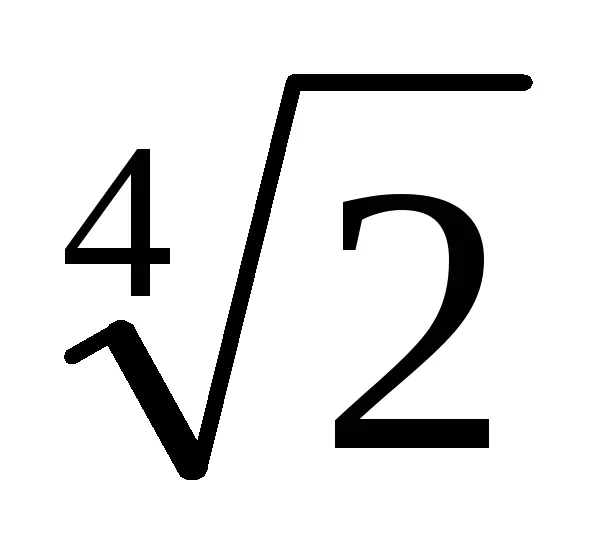
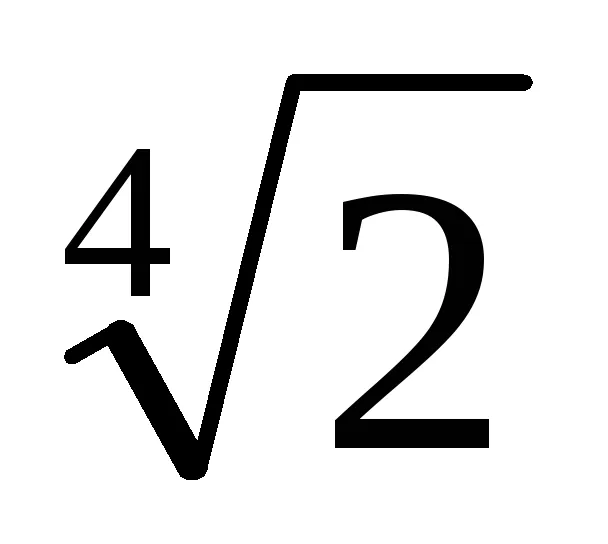
2. Намерете линейно разширение на НОД (

(X), р (х)) при използване на Euclidean алгоритъм.

-X-2 -

х - = Q3 (х)

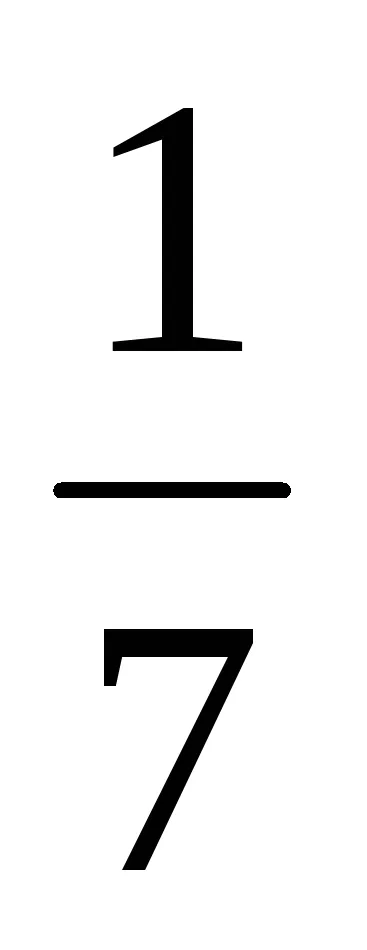
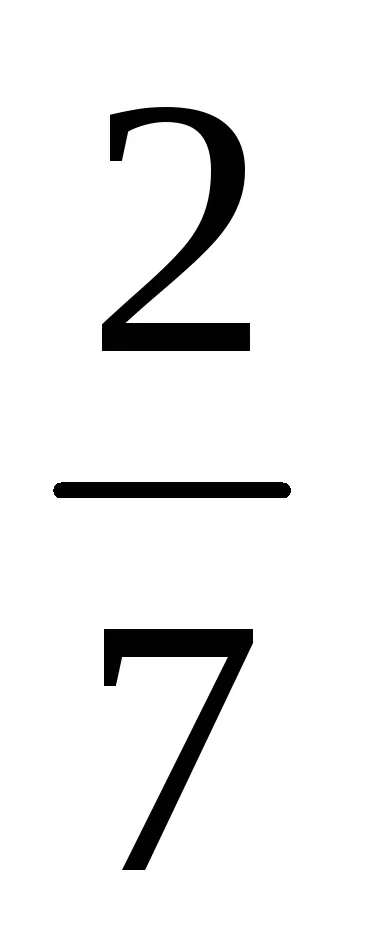
Така че ГРУ (

(X), р (х)) = R2 = 7. Ние намери линейно разширение.

Пишем последователност Евклид, като се използва система за означаване на полиноми.

р (х) =

(X) · q1 (х) + r1 (х)r1 (х) = Р (х) - (X) · q1 (х)

(X) = r1 (х) · q2 (х) + r2 (х) r2 (х) = (X) - r1 (х) · q2 (х)

Заместването в уравнение 7 = r2 (х) =

(X) - r1 (х) · Q2 (х) r1 стойност остатък (х) = р (х) - (X) · q1 (х), ние се получи линейна трансформация след разлагане GCD ((X), р (х)): 7 = р (х) · (- q2 (х)) + (X) · [1 + q1 (х) · q2 (х)]. Ако заместим в последното равенство вместо символи, съответстващи полиноми и вземе предвид, че р () = 0, имаме:

(1 -

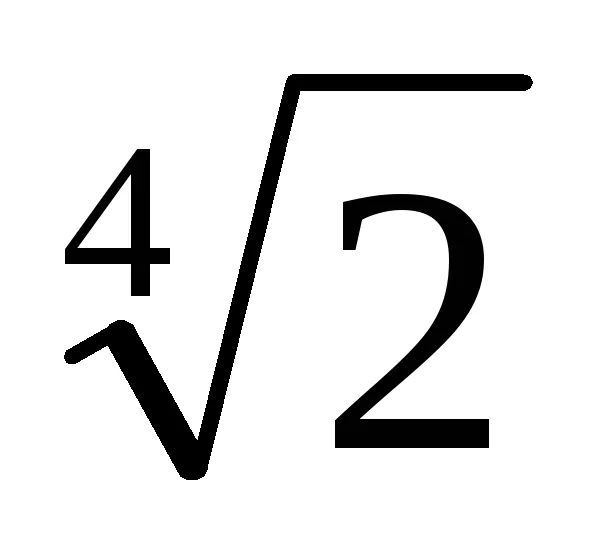
+) · (-+ 2+ 3+ 1)] = 7 (1)

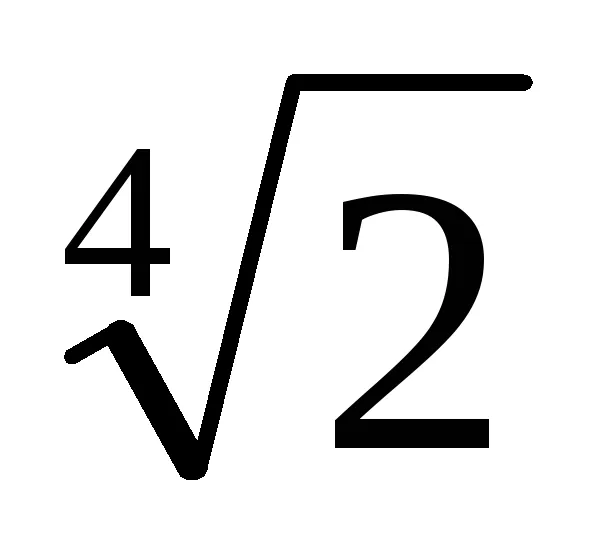
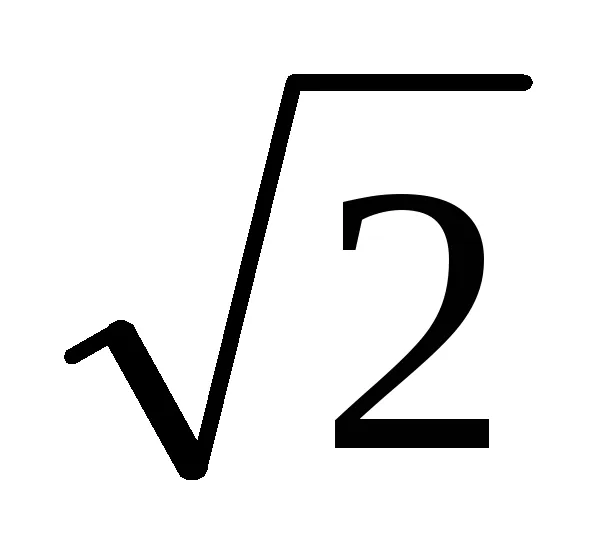
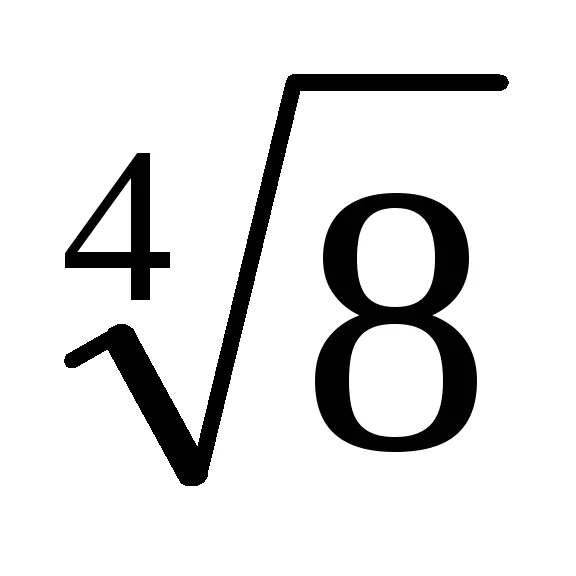
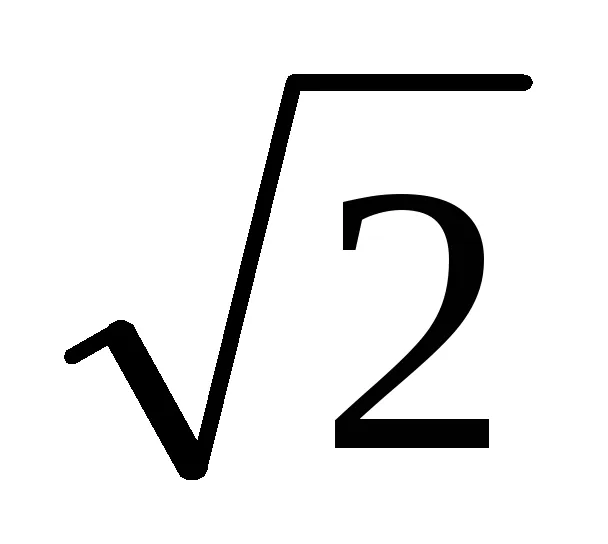
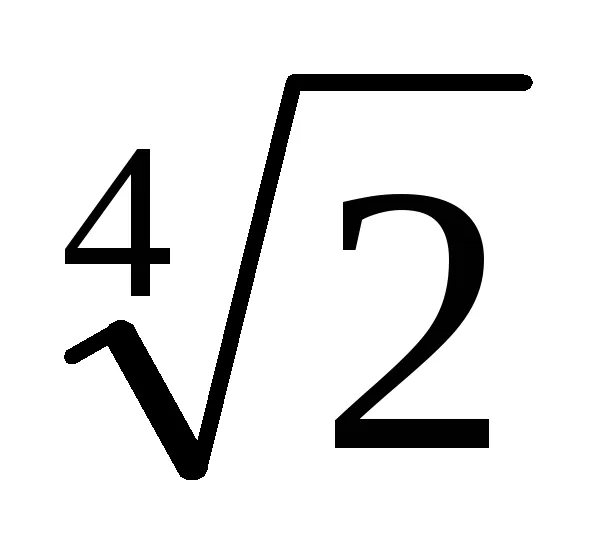
3. От уравнение (1) означава, че ако знаменател, умножена по броя на Тт = [1 + (-

+ 2+ 3+ 1)], ние получаваме 7. По този начин,

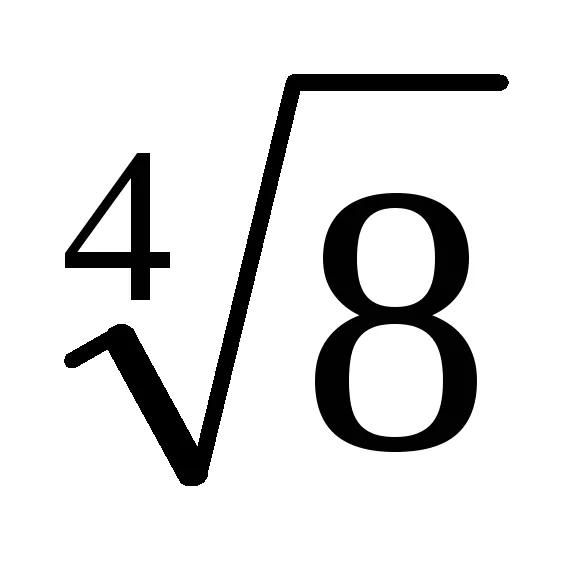
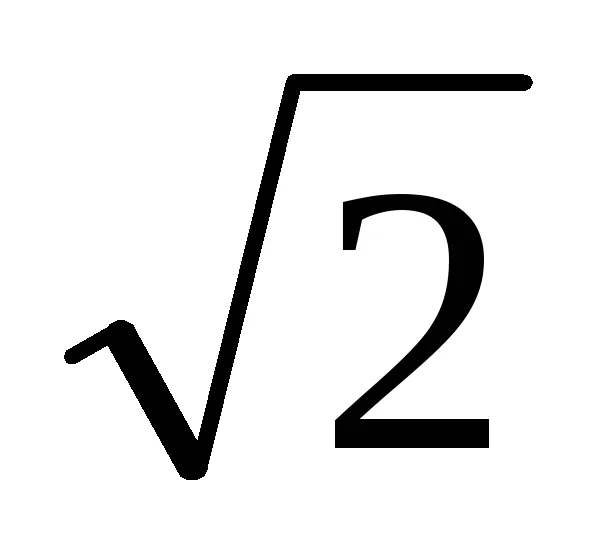
МЕТОДИКА 16. Урок Относно: Стандартен изглед полином

Вид на урока: за проверка и контрол на знанията и уменията урок

- проверят полином умения водят до по образец

- да развиват учениците логическо мислене, внимание

1. Изпълнете изречения:

а) експресия, съдържащ сума на едночлени посочени ... (полином).

б) полином, състояща се от стандартни едночлени и не съдържа такива условия се нарича ... (стандартна полином).

в) най-висока степен на едночлени, които влизат в полином се нарича стандартен формуляр ... (степента на полинома).

г) Преди определяне на степента на необходимост ... (за да го занесете в стандартна форма).

г) За да се определи стойността на полином необходимостта да се направи първо ... (представете си полином по образец), втора ... (посочете стойността на променливата в израза).

2. Намерете стойността на полином:

3. Носете си полином по образеца:

4. Носете си полином на стандартен формуляр и да разберете за какви стойности на х стойността е 1: