прогнози Строителство аксонометрични предмети призматична и пирамидална форма

Начало | За нас | обратна връзка

издатини строителство аксонометрични започват от базовата изображението или характерни лицата обект, т.е. равнинни фигури разположени в една равнина: отпред, или хоризонтален профил. Ето защо, нека първо да разгледа образа на равнинни фигури.

Пример 1. Изграждане аксонометрична проекция на равностранен триъгълник (фиг. 3.44 и фиг. 3.45).

1) триъгълник е разположена в предна равнина. В х "определя от двете страни на точката 0 'на оста Z', сегментите б / 2, равен на сумата от г - страна на триъгълника, и на Z 'ос - на височина Н. Получените точки са свързани с права линия сегменти.

2) триъгълник е разположена в хоризонтална равнина. Както х "ос нанасят срещу точката 0 'на оста Z сегменти б / 2, равни страна на триъгълника сумата В- и у' - височина Н на изометричното. (Фигура 3.44) и половината проекция на височината (Н / 2 ) - за предната dimetric (фигура 3.45) ..

3) триъгълник е разположена в профилната равнина. Чрез забавяне страна половина у ос (Ь / 2) за предната и странична проекция dimetric В за изометрично, и по-Z 'ос - на височина Н.

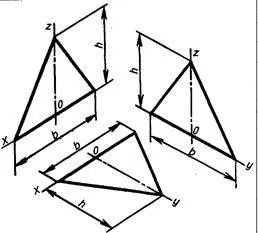
Изображение на равнобедрен триъгълник в правоъгълна изометричното

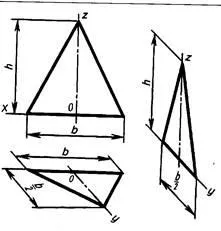
Изображение на равнобедрен триъгълник в предната проекция dimetric

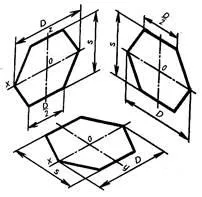
Снимка на правилен шестоъгълник в изометрия

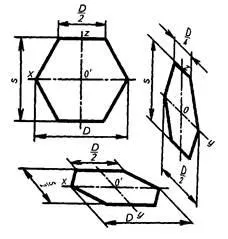
Снимка на правилен шестоъгълник в предната проекция dimetric

Пример 2. Конструиране аксонометрични проекции на правилен шестоъгълник (фиг. 3.46 и фиг. 3.47).

1) шестоъгълник намира в челната равнина. Както х "ос симетрично при 0" положи радиусите на описаните окръжности (D / 2) е равен на размера на шестоъгълника, и Z-ос симетрично при 0 - сегменти S / 2, равна на половината от разстоянието между срещуположните страни на шестоъгълника (които могат да бъдат определени от формула S = 0866 V).

Чрез точките, получени в Z 'ос, проведени с права, успоредна на оста х и Z-ос симетрично "лежеше на техните дължини, равна на половината на шестоъгълника (D / 2). Получените шест точки, свързани с права линия сегменти.

2) шестоъгълник разположен в хоризонтална равнина. Строителство се извършва, както е обсъдено по-горе, с единствената разлика, че на разстояние S между противоположните страни (за пред проекция dimetric S (2)) нанесени върху оста у.

3) шестоъгълник намира в профил равнина. В този случай, размерът V (за пред проекция dimetric - D / 2) се нанася върху оста у и размер S - по ос В на тази издатина се намаляват наполовина на шестоъгълника също са разположени успоредно у ос (размер V / 4).

Пример С Изграждане на аксонометрични проекции на призми (фиг. 3.48 и фиг. 3.49).

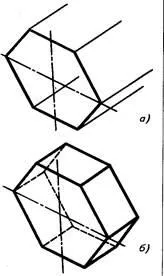
Изображение редовен шестоъгълна призма в перспектива

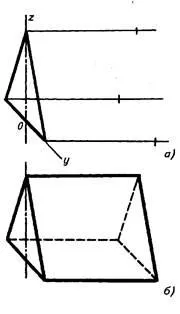
Изображение триъгълна призма на изпъкналостта в челната dimetric

Първо, изграждане на видима проекция основа, такава като в равнина Z 0 Чрез върховете извършва линии успоредни на оста Х, и те са маркирани на разстояние от височината (дължина) на призмата (фиг. 3.48, а и фиг. 3.49, а).

Получените точки са свързани с прави отсечки и обкръжават appar- тия ред и невидим схема (фиг. 3.48, б, и фиг. 3.49, б).

Пример 4. Конструиране на аксонометрични проекции на редовни пирамиди (фиг. 3.50 и фиг. 3.51).

Първо, изграждане на проекция пирамида база и през точката 0 '- центъра на тежестта, получен в равнината на фигурата - се извършва Z' ос. От гледна точка 0 на Z 'ос относно височина на пирамидата (фиг. 3.50, а и фиг. 3.51, а).

Получената точка (връх проекция пирамида), свързан към базовите върховете на издатъците. Накрая обгради видими и невидими линии контур (фиг. 3.50, б, и фиг. 3.51, б).

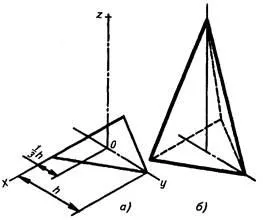
Изображение редовен триъгълна пирамида в перспектива

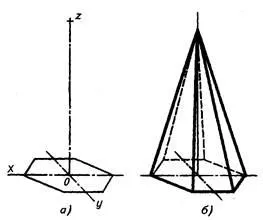
Изображение редовен шестоъгълна пирамида фронтална проекция dimetric