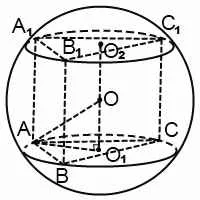
Prism е вписан в сфера
Prism е вписана в играта, ако всички негови върхове лежат на повърхността на топката (на терена). В този случай ние казваме, че топката е описан около призма (или призми близо сфера описани).
Prism може да се впише в една сфера, ако и само ако, когато
1) с права призма;
2) в близост до основата може да бъде описан като кръг.

От това следва, че топката може да се впише права триъгълна призма, правилна призма.
Тъй като четириъгълник може да бъде вписан в окръжност, ако сумата на противоположните ъгли равна на 180 °, с права правоъгълна призма може да бъде вписан в сфера само при това условие.
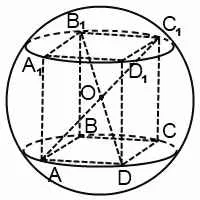
По-специално, паралелепипеди, описани балон може да бъде приблизително формата на правоъгълен паралелепипед само. център на топката в този случай - до точката на пресичане на диагоналите на кутията.
Като цяло, в центъра на окръжност областта около призмата намира на средата на височината на призмата, минаваща през центровете на кръгове около основата му. Центърът на топката може да се опише в рамките на призмата, през призмата и е на страната на неговото лице.
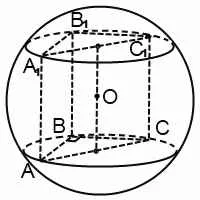
Например, за триъгълна призма, в която ъгълът ABC - права описано топка център лежи върху страничния ръб, на височина, която свързва средите на хипотенузата на призмата в мотивите.
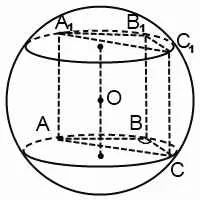
Ако ъгъл ABC на - тъп, центъра на окръжност областта за триъгълна призма на призмата се намира.