Пример за изчисляване на риска и очакваната възвръщаемост на портфейл от ценни книжа, две

Предложи че инвеститорите провеждат предварително проучване на пазара на ценни книжа, оценката на очакваната възвръщаемост R, стандартните отклонения на ценните книжа, от всеки вид, и съотношението между тях с ценни книжа. Сега, инвеститорът трябва да бъде един инвестиционен портфейл с най-висока доходност и нисък риск. За тази цел, от една страна, да установи комуникация между очакваните стойности дават ценни книжа и очакваната доходност на портфейла се състои от тези документи, и второ, да се установи връзката между стандартните отклонения на портфейла и неговите компоненти - на ценни книжа; третата стъпка трябва да бъде да диверсификация на инвестициите, като например модела на Марковиц, който ще бъде разгледан по-долу. Въпреки това, като подготовка за този преглед, ние ще решим по-прост проблем - изчисления на риска и портфейлни връща с вече определените характеристики на неговите компоненти, избрани от всички критерии.

разгледа хипотетичен пример за илюстриране на риска от изчислителните процедури и портфейлни възвръщаемост. Нека инвестиционен портфейл на инвеститора се състои от акции на две дружества А и Б, със следните характеристики, посочени в таблица. 4.2. Необходимо е да се изчисли очакваната възвръщаемост и потенциалния риск от инвестиране в тези запаси.

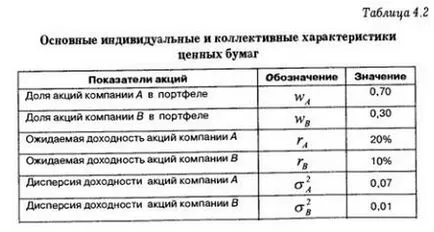
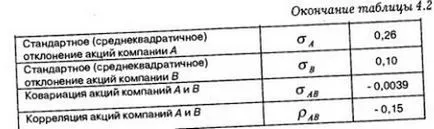
Очакваната доходност на портфейла от ценни книжа се изчислява като средно претеглената стойност на очакваната възвращаемост на съставните му ценни книжа. Съответно, очакваният добив на портфейла зависи от пропорциите, в които са представени компонентите - ценните книжа на даден вид. В този пример, инвеститор от съществуващите 10000 рубли. поставя 7000 рубли. И в акциите на компанията и 3000 рубли. в акциите на компанията в (тегло на акциите на дружества А и Б в портфейла е 70% и 30%). При стойности добиви от 20% и 10% на компонентите портфейл Добивът средната портфейл е 17%.

За оценка на риска на портфейла и изчисляване на дисперсията на портфейл, и използването на формула (4.9) за изчисляване на дисперсията на портфейла:

Изчислено за съотношение дисперсия показва едно много важно свойство: портфолио дисперсия зависи не само от стандартното отклонение добиви ценни книжа, но и на ковариацията между тях (трябва да се отбележи, че ковариацията е симетрични, т.е. IMP,

Дисперсията показва как летлив доходността на ценна книга, ковариацията характеризира степента на корелация между доходността на две статии. Положителна корелация между добивите на ценни книжа увеличава дисперсията, и по този начин риска от портфейла. Отрицателна корелация, а напротив, намалява разсейването на портфейла, което, разбира се, се потвърждава от практиката на пазара на ценни книжа. Ако цените на активите са променени в една посока, като същевременно намали цената на инвеститора ще загуби много повече, отколкото в случаите, когато цената на някои от най-ценните книжа падат, а други - растат. За този случай е равна на дисперсията на портфейла:

Стандартното отклонение на портфейла има същото тълкуване като стандартно отклонение на ценната книга. Стандартно отклонение на портфейла - е мярка, на която инвеститорът оценява вероятното отклонение на действителната доходност от очакваното, т.е. оценява риска от "отклонява" от очакваната - не получите очаква приходите от продажба на ценни книжа. Средната очаквана възвръщаемост счита портфейл е 17.0%. Когато се очаква стандартно отклонение от 18.33% добив на портфейла да бъде в границите от 35.33% до -1.33% с вероятност от 68% (нормална, Гаусово разпределение вероятност).