Преизчисление част от мол в масата

Според данните, които се конструира Isobar графика на кристализация начало температура на системата за състав в координати T - NA (фиг.1).

Преизчисление мол фракции в масата

Мас фракция на веществото в двукомпонентна система е съотношението на масата на веществото на общото тегло на системата.

Разделяне това уравнение от теглото на компонент А, получаваме

Представяне компонент тегло, както продукта от компонент молекулното тегло на броя на моловете, да получават

Моларното масата на компонента в двукомпонентна система е съотношението на броя на моловете на компонента на общия брой молове на системата.

Следователно, съотношението на мол от компоненти е равен на съотношението на броя на моловете на съответните компоненти.

Заместването на уравнение (2.5) до (2.3), ние получаваме формулата за превръщане на молната фракция на компонента в масово:

резултати преобразуване са показани в таблица. 2.1.

Получените данни се конструира изобарно диаграма в координати T - А (Фигура 2).

Чрез кристализация диаграма сграда охлаждане криви (Фигура 3) вариант на системата в точките, принадлежащи към криви данни, описани по правило Gibbs фаза.

Ако хетерогенна система налягане и температура във всички фази на същото, и на броя на моловете на всички компоненти във всяка фаза е постоянен, то се нарича фаза равновесие състояние. Фаза на равновесие състояние е равна химически потенциал на компонента във фаза към стойността на всяка друга фаза.

За да се опише състоянието на хетерогенна система, е необходимо да се знае температура, налягане и концентрацията на компонентите във всяка фаза. Но ако установената фаза равновесие, само част от тези променливи са независими, като концентрациите на компонентите в отделните фази са свързани чрез уравнението (4.1). Броят на независимите променливи, необходими за да се опише състоянието на равновесие на хетерогенна система, наречена дисперсията, или броя на термодинамични степени на свобода на системата. Вариации на системата (# 969;) също така определя редица независими променливи, които могат да бъдат произволно (в определени граници), за да се промени, без да се нарушава състоянието на системата, тоест, без да се променя броя и вида на фази в него. Вариант на системата зависи от броя на компонентите и се определя от правилото фаза Gibbs

# 969; = К - F 2 - R - L. (4.2)

където К е - броя на компонентите;

R - броят на химични реакции в системата;

L - броят на допълнителните свързващи уравнения между компонентните концентрации.

В тази книга, ние считаме система без никакви химически реакции и без допълнително ограничение уравнения, които също се изследват при постоянно налягане. Ето защо, в уравнението на Гибс ще бъде:

Използването на това уравнение, да се изчисли дисперсията на охлаждащите криви (Фигура 3) и fusibility схема (Фиг.1). Изчислението е дадено до (Фигура 3)

Сключването на правилото за лост.

Масата на утаените кристали от стопилката по време на охлаждане, може да се определи като се използва правилото на лоста. Заключението на това правило се прилага за точка O. За тази форма на уравнението на материалния баланс на компонент В при постоянна температура.

m # 966; Б (О) = mrastvora # 966; B (L) + mkristallov # 966; В (К) (5.1)

Заместването на уравнение (5.2) до (5.1), получаваме

(+ Mrastvora mkristallov) # 966; Б (О) = mrastvora # 966; B (L) + mkristallov # 966; В (К) (5.3)

Решаването на последния уравнението за маса от кристали:

mrastvora # 966; Б (О) + mkristallov # 966; Б (О) = mrastvora # 966; B (L) + mkristallov # 966; В (К)

От получената уравнението е със скорост от:

;

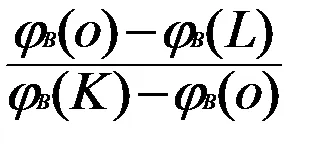
СО = 20, OL = 45 = 2-mrastvora MKR

Да разгледаме система равновесие, състояща се от две фази - течност и твърдо вещество. Нека всяка фаза е истинското решение. Когато равновесие фаза

химически потенциал на компонент във всяка фаза е в зависимост от температурата, налягането и компонент активността

Когато μk 0, х (Т, Р) и μk 0 телевизия (Т, п) - химически потенциал на чист компонент течност и твърди състояния при дадена температура и налягане;

ак и ак х телевизия - активен компонент във фазите на равновесие.

Като се има предвид (6.1) и (6.2), (4.1) може да се трансформира в

При постоянна температура и налягане

От (6.4) следва, че съотношението на активния компонент във фазите на равновесие при постоянна температура и налягане, - правото на фаза равновесие.

Ако при дадена температура и налягане добавен в една от фазите на редица компонент к, това ще доведе до неговото преразпределение между фазите, така че съотношението на активния компонент в равновесието стабилен отново остават непроменени. Когато температурата или налягането промени, системата ще отиде в друга състояние на равновесие, при което съотношението на промяна на активния компонент във фазите на равновесие и ще се измести равновесието.

Да разгледаме, като промяна в температура при постоянно налягане промяна засяга състава на фазите на равновесие. За да изрази тази в уравнение (6.3) чрез мол фракции на дейност

Получената уравнението за температура диференцират

Съгласно уравнението на Гибс-Хелмхолц

при което - промяна в химическата потенциал на чистия компонент при преминаване от твърдо вещество към течност;

- моларно топлината на топене компонент.

С помощта на уравнението (6.7), получаваме

Последният уравнението в диференциална форма описва ефекта на температурата върху състава на равновесие при изобарно изместване на фазата на равновесие, по време на прехода от състояние на равновесие при една температура в състояние на равновесие при различна температура.

Твърдите разтвори форма компоненти, подобни на химични и физични свойства и имат същия тип кристална решетка. Ако компонентите в твърда фаза са неразтворими една в друга, тогава течния разтвор подчертано кристали на чисто вещество. В този случай е налице равновесие: течен разтвор двукомпонентен и кристали на един компонент (NK тв = 1, # 947; к тв = 1), и уравнението става

Интегриране на това уравнение, като се предполага, че не е зависима от температурата

Тук - кристализация температура на разтвора на чист компонент и температурата на кристализация на чисто вещество. Уравнение (6.10) в интегрална форма описва ефекта на температурата върху равновесие "течен разтвор - кристали компонент". Ако течната фаза в близост до идеални свойства на разтвор на (# 947; к х = 1), след това уравнение (6.10) се записва под формата

Последният уравнение се нарича Шрьодер уравнение, където - молната фракция на компонент в течния разтвор се намира в уравнение с неговите кристали, т.е. концентрацията на компонент в наситен разтвор или разтворимостта на компонент при к

От уравнение Schroeder, че в случай на идеални решения разтворимост на компоненти се увеличава с повишаване на температурата.

уравнение на Шрьодер може да се използва за различни задачи:

1. Когато е известно кристализация температура на чистия компонент и посочения състав на температурата на топене кристализация, след това уравнение (6.11) може да се изчисли топлина на топене мол компоненти к:

и могат да бъдат определени от диаграмата на системата.

2. Ако е известно, моларното топлината на слят компонент, уравнение (6.11) може да бъде решен за температурата, при която стопилката на кристалите стане видно компонент к:

3. Изчисляване на понижаване на температурата на кристализация на компонентите се топи на различен състав -:

Уравнението (6.11) за компонент А:

От уравнение (6.14)

За разредени разтвори (NK телевизия → 1, # 947; к телевизия → 1)

В разредени разтвори. така последното уравнение може да се запише с помощта на г-скала

Количеството в уравненията (6.15) и (6.16) до стойности, експресиращи състава на разтвора. Наречен cryoscopic константа, която зависи само от свойствата на компонент А.

1. Киселева EV Karetnikau GS Кудряшов IV Събирането на примери и проблеми във физически химия. Proc. Прибавка за Chem-първичен процес. vuzov.- пети ред. Ревизираната. и вътр. - М. изпълнителния. седм. 1983.- 456 стр.

2. Лекции по физикохимия (доцент Uritskaya АА).

Равновесие "Фуга (стопилка) - кристали" в двукомпонентна система на

Учителят: Uritskaya AA

1. Задачата на курсов проект

1.1. състояние проблем

1.2. първоначалната информация

2. Превръщане част от мол в масата на компонент А. Конструиране Isobar диаграма в координати T # 966 А

3. Описание на диаграмата по регионите fusibility

4. Охлаждане криви

4.1. правило Gibbs фаза

5. Определяне на кристална маса

5.1. Сключването на правилото за лост

6. Уравнение Шрьодер

6.1. Извеждане на уравнението

6.3.1. Изчисляване на моларните топлини на топене вещества А и В

6.3.2. Изчисляване на кристализацията започне температури на компонентите А и В

6.3.3. Изчисляване на коефициентите на активност на компонентите А и В

6.3.4. Изчисляване cryoscopic константи А и Б вещества

Препратка към курсов проект

1. Експерименталните данни за всеки вариант трябва да се вземат от таблицата. "Зависимост начало температура на кристализация от стопилка в състава (в мол фракции)." Според тези данни, за да се изгради изобарно диаграма (Т - NA).

2. извличане на уравнението за преобразуване на част от мол в масата на компонента А. Осигуряване таблична реализация на мол фракция (НС) в масовите части (# 966 А) и изграждане изобарно диаграма в координати T - # 966; A.

3. Описание на диаграма fusibility район.

4. Draw всички видове охлаждане криви (криви в координати "температура - време" и ги описват, на базата на правилото за фаза Gibbs).

5. изход уравнение за изчисляване на масата на фазите на равновесие (лост правило) в областта на диаграма (Т - # 966 А), при което има: а) кристали на компонентите А - стопилка; б) компоненти на кристалите - стопи.

6. Изчислете масата на утаените кристали при охлаждане двекилограма стопилка. Съставът на стопилката е дадено от учителя.

7. извлече уравнението Schroeder и изчисляване на моларен топлина на топене на веществата А и В при сближаването на идеалното решение (NK → 1).

8. Изчисли от уравнение Шрьодер, кристализация началната температура на компонентите А и В от стопилки с различен състав. Сравнете експерименталните криви кристализация (графика T - NA) с изчислява.

9. изчисляват коефициентите на активност на компонентите А и В в разтвор с NA = 70% и NB = 67.5%.

10. При понижаване на температурата в началото на кристализация на вещества А и В от разтвор състав NA = 70% и NB = 67.5% определи постоянна стойност cryoscopic вещества А и Б съгласно експерименталните данни.

За да се реши този проблем се получават следните данни: двукомпонентна система е LI2 CO3 стопена сол (съединение А) и К 2СО 3 (вещество Б). Тези вещества съответстват моларна маса MA = 73.89 • 10 -3 кг / мол, MW = 138 • 10 -3 кг / мол. температура зависимост от началото на кристализация на разтвора от състава на разтвора е показано в таблица. 1.1.

А моларен фракция,%

Температурата на начало на кристализация, K

Преизчисление мол фракции в масата

Разделяне това уравнение от теглото на компонент А, получаваме

Представяне компонент тегло, както продукта от компонент молекулното тегло на броя на моловете, да получават

резултати преобразуване са показани в таблица. 2.1.