Построения с линийка и пергел

Конструкции с владетел и компас - раздел на евклидовата геометрия. известна още от древността. Задачите на изграждането на компас и владетел се считат за идеални инструменти, по-специално:

Линията още няма разделения и е с лице на безкрайна дължина, но само един.
Компасът може да бъде произволно големи или малки разтвор произволно (т.е., може да се направи произволен радиус кръг).

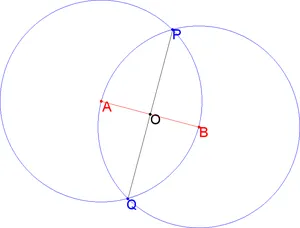
Разделяне на половина дължина

Предизвикателството за разполовяване. С помощта на линийка и компас разделят сегмент AB на две равни части. Едно решение е показано по-долу:

Компаси притежават окръжност с център в точките А и В радиус AB.
Намерете пресечните точки P и Q два вградени кръгове (дъги) на.
Чрез провеждане отсечка или линия, преминаваща през точките P и Q.
Намираме се изисква средата AB - пресечната точка на AB и PQ.

Официалното определение

Задачите на сграда се считат за множеството от всички точки в равнината, на снимачната площадка самолет на всички линии и набора от всички кръгове на повърхността, върху която се допускат следните операции:

Изберете точка от множеството от всички точки:
1. произволна точка
2. произволна точка от дадена линия
3. произволна точка на предварително определен обиколката
4. точката на пресичане на две дадени линии
5. пресечната точка / докосване дадена линия и определен кръг
6. точката на пресичане / контакт на две среди даден
"С помощта на линийка", за да се разпределят директно от снимачната площадка на всички линии:
1. произволен ред
2. произволна линия, минаваща през дадена точка
3. права линия, минаваща през две дадени точки
"С помощта на компас" връхна точка обиколка на множеството кръгове:
1. произволно кръг
2. произволна кръг центриран при предварително определена точка
3. произволна кръг с радиус, равен на разстоянието между две точки
4. окръжност с център в даден момент и с радиус, равен на разстоянието между две точки

По отношение на проблема е дадено от набор от точки. Изисква се от определен брой операции на броя на допустимите операции са изброени по-горе за изграждане на друг набор от точки, разположени на предварително определено съотношение с първоначалният комплект.

Решение за сграда се състои от три основни части:

Описание на метода за изграждане на даден набор.
Доказателство, които отличават конструирана, както е описано, е наистина в предварително определено съотношение с първоначалният комплект. Обикновено, изграждането на доказателство се произвежда като нормална доказателство на теоремата, въз основа на аксиоми и други теореми доказани.
Анализ на описания метод за конструиране на неговата приложимост в различни изпълнения, първоначалните условия, така и за не-уникалност уникалност или разтвори получи описани.

известен проблем

Проблемът за конструиране Аполоний кръг докосва три предварително определени окръжности. Ако никой от посочения кръг не лъже в друг, този проблем има 8 съществено различни решения.
Задачата на изграждане Брахмагупта четириъгълник вписан на четирите му страни.

Изграждане правилен многоъгълник

Изграждане на равностранен петоъгълник

Антични geometers били известни методи за конструиране на редовни н -gons за ,, и.

През 1796 г. Гаус показа възможността за изграждане на правилни н -gons кога, къде - различен прости числа ферма. През 1836 г., Пиер Wantzel се оказа, че и други редовни полигони, които могат да бъдат изградени от владетел и компас, не съществува.

нерешени проблеми

Следващите три проблемите на строителството са били пуснати в древността:

ъгъл Trisection - произволен ъгъл разделена на три равни части.
Удвояването куб - изграждане на куб ръб два пъти повече от обема си от куба
Squaring кръга - за изграждане на квадратен равни по площ от този кръг.

Само в ХIХ век е доказано, че и трите са нерешими проблеми, използвайки само владетел и компас. Въпрос възможността за изграждане на напълно решен чрез алгебрични методи, основани на Галоа теория.

Друг известен нерешим използване компас и владетел задача - да се построи триъгълник от три ъглополовящи на предварително определена дължина. [1] Освен това, този проблем остава нерешен дори в trisektora на присъствие. [2]

Възможно и невъзможно да се построи

Всички конструкции са нищо друго, освен решенията на всяко уравнение. където коефициентите на уравнението, свързани с предварително определени дължини на сегментите. Поради това е подходящо да се говори за изграждане на - графичното решение на уравнението на определен тип. Като част от по-горе изисквания, следната конструкция:

С други думи, това е възможно да се изгради брой, равен на аритметични изрази, с помощта на корен квадратен от входните числа (сегментни дължини). Например,

Ако само един сегмент с дължина, не е възможно да си представим в тази форма (оттук и невъзможността на двоен куб).
Възможност за изграждане на редовната 17-гон От косинус на ъгъла:

Вариации и обобщения

Конструкции с един компас. От теоремата на Мор - Mascheroni с помощта на компас, може да се изгради във всякаква форма, която може да се изгради компас и линийка. Когато това се счита за да бъде построен направо, ако две точки са посочени в него.
С помощта на една и съща линия. Лесно е да се забележи, че единственият проективна неизменна на строителство може да се извършва с един ред. По-специално, не е възможно дори да се раздели отсечката на две равни части, или да се намери центъра на изготвен кръга. Но присъствието на самолета предварително проведено от окръжност с център отбелязана с владетел може да се направи със същата конструкция като владетел и компас (Poncelet теорема -. Щайнер (на английски)), 1833 г. Ако линията има две степени, строителството с помощта на нея еквивалентни конструкции с владетел и компас (важна стъпка в което доказва, че Наполеон е направил).
С помощта на инструментите за хора с увреждания. Проблемите на този вид инструменти (за разлика от класическата формулировка на проблема) се считат за не идеални, но ограничени: права линия през двете точки с владетел може да се извършва само при условие, че разстоянието между тези точки не превишава определена стойност; радиус кръгове проведени с шублер могат да бъдат ограничени в горната, долната част или и двете на горната и долната част.
На строителни с плоска оригами. см. правилата Hudzita

интересни факти

Моделът на флаг е описан като Иран конструкция с линийка и компас [3].

Dynamic заявление Геометрия ви дава възможност да се изгради с владетел и компас на компютър.

Построения с линийка и пергел - е