Понятието производно, геометричния смисъл и механична

Нека функция у = F (X), определена в точка x0 и определен квартал, х - от тази точка съседство. Представяме означението: разликата х - x0 е означен с # 916; х и се обадете на нарастване на аргумента. и F на разлика (X) - F (x0) е обозначен с # 916; у и nazovemprirascheniem функция.

По този начин, # 916 х = х - x0. # 916; у = е (х) - F (x0). на равенство # 916 х = х - x0 ние получаваме
х = x0 + # 916 х, след това # 916; Y = F (x0 + # 916 х) - F (x0).

Производно с F функция (х) при x0 е граница на съотношението на функцията на нарастване на нарастване на аргумента, когато нарастването на аргумента клони към нула.

Производно Обозначена е "(x0).

Пример 1: Виж производното на функцията F (X) = х 2 в точка x0 = 3.

Ако е "(x0) съществува, тогава се каже, че F функция (х) е диференцируема в точка x0 на. Ние се установи връзка между диференцируема функция е (х) при x0 и непрекъснатост в този момент. Припомнете си, че F функция (х) е непрекъсната в точка x0 на, ако е определено в точка x0 и някои от неговите околности и след равенство:

Преформулиране на това определение, като се използва аргументът на нарастване на концепцията и функцията на нарастване. От това уравнение получаваме:

С други думи, F функция (х) е непрекъсната в точка x0 на. ако безкрайно нарастване на аргумента съответства на функция безкрайно увеличение.

Теорема. Ако F функция (х) е диференцируема в x0, към който е непрекъснато в този момент.

Забележка. Ако F точка x0 функция (х) е непрекъсната, а след това в този момент на функцията може да бъде получен, както е видно от следния пример.

Пример 2. F функцията (х) = | х | е непрекъсната в точка x0 от = 0, тъй като.
Ние показваме, че тази функция не е производна в точка x0 на.

не съществува, т.е. е (х) не е диференцируема в точката x0 = 0.

Разглеждане на геометрична смисъла на производно.

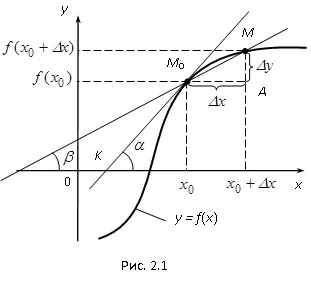
Фиг. 2.1 показва графика на непрекъсната функция у = е (х). M0 точка данни има координатите x0. F (x0), друга точка на графиката М - координира x0 + # 916 х, F (x0 + # 916 х). Директен M0 М е пресичане на линията Y = F (х), тя е наклонена спрямо оста на ъгъл Ox # 946;. Нека F '(x0) съществува, т.е. има определен брой. от # 916; М0 УО получи (известно е, че TG # 946 - наклона на правата линия M0 М). ако # 916 х → 0, се движи точка М на графиката на функция у = F (х), приближаващи точката M0. където сечащ M0 М, завъртане около точката M0. има за цел да вземе крайното положение, т.е. да съвпадне с допирателната M0 K, докато # 946; → # 945; (# 945 - ъгълът между тангентата и оста M0 К Ox), TG # 946; → TG # 945.

По този начин, но TG # 945; = К е наклонът на допирателната M0 К.

По този начин, наклонът на допирателната към крива у = F (х) при x0 с абсцисата е производно е (х) при x0. F '(x0) = к = TG # 945.

Това е геометрична тълкуване на производно. Очевидно е, че уравнението на допирателната M0 К е в следния формат:

Ние пристъпва към разглеждане по механичен смисъл производно.

Нека точката на маса се движи праволинейно неравномерно законно S = е (т), където т - време, S - път пътува през времето точка тон.

Да предположим, че в момент t0 точка е в M0 позиция (фиг. 2.2). Ние поза на проблема: да се определи скоростта на материалната точка в момент t0. Помислете за друг момент t0 + # 916; т. По време на точка от време t0 премества пътеката е: S0 = F (t0), за (t0 + # 916; т) Travel разстояние S = F (t0 + # 916; т), и точката е в положение М, след това за времето # 916; т пътя, изминат M0 М и е равна на:
S - S0 = F (t0 + # 916; т) - е (t0) = # 916; S.

Средната скорост на Вав ppomezhutok време # 916; т е равно на :. Въпреки това, средният процент може да бъде различна, в зависимост от времевия интервал # 916; т. Оценка на времето за време t0 (означен V (t0)) е скоростта на ограничение, когато средната VAV # 916; т → 0. По този начин,

Заключение. Производното на пътека S = F (т) в момент t0 е скоростта в момента от време t0.