политропно експонат

Крива на термодинамични диаграми, илюстриращи политропно процес, наречен "polytrope". За идеално уравнение газ политропно може да се запише като:

където р - налягане, V - обем на газ, п - «политропно индекс".

. Когато - специфичната топлина на газа в процеса, и - специфичната топлина на газа, съответно, при постоянно налягане и обем.

Различните стойности на политропно експонентата

Стойността на индекса политропно

Въпреки, че този случай е без практическа стойност за най-често срещаните инженерни приложения, на политропно индекс може да бъде отрицателна в някои специални случаи, разгледани, например, в някои щати в плазмата астрофизиката. [1]

Това изобарен процес (протичащ при постоянно налягане)

Този процес изотермични (протичащ при постоянна температура)

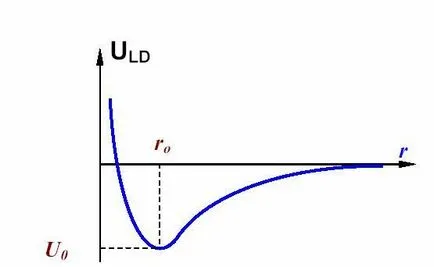
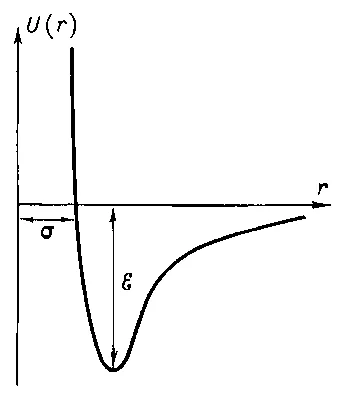
11. Графика Ленард-Jones потенциал.

потенциал Ленард-Джоунс (потенциал 6-12) - прост модел на чифт взаимодействие на неполярни молекули, описваща зависимостта на енергията взаимодействието на две частици между тях на разстояние. Този модел е доста реалистични свойства предава реално взаимодействие сферични неполярни молекули и поради това се използва широко в изчисленията и чрез компютърна симулация. За първи път този тип сграда е предложен от Ленард-Джоунс през 1924 година. [1]

потенциал Ленард-Джоунс е написано, както следва:

при което - разстоянието между центровете на частиците, - дълбочината на потенциал кладенеца, - разстоянието, на което енергията на взаимодействие става нула. Параметрите и характеристиките на веществото са атома. Характерните формата на потенциала е показано на фигурата, е най-малко една точка.

За големи молекули са привлечени, което съответства на термина в Eq. Тази зависимост може да се обясни теоретично и е причинена от ван дер Ваалс сили (дипол-индуциран дипол взаимодействия).

В къси разстояния молекулите отблъскват взаимно дължи на взаимодействието обмен (поради натрупване на електронните облаци молекулата започва да прокара изключен), което съответства на член. Този специфичен вид отблъскване потенциал, за разлика от типа на привличане потенциал, липсва теоретична основа. По-разумно е експоненциална зависимост [цитиране необходими 980 дни]. Въпреки това, отблъскваща потенциал Ленард-Джоунс по-удобно в изчисленията, защото, който оправдава използването му.

31. Лема на линейната независимост на ортогонална система. Процесът на Грам-Шмид ортогонализиране.

Грам-Шмид процес - най-известен ортогонализиране алгоритъм. при което lineynonezavisimoy система stroitsyaortogonalnaya sistematakaya че kazhdyyvektor би линейно изразена чрез, т.е. матрицата преход от AI> на BI> -verhnetreugolnaya матрицата. По този начин е възможно да се гарантира, че системата е двупосочен> е ортонормирана ichtoby диагоналните елементи на матрицата на преход са положителни; тези условия системата BI> imatritsa преход еднозначно определени.

Този метод е приложим към системата за отчитане на вектори също.

Метод Грам - Schmidt може да се тълкува като разширение nondegenerate vproizvedenie ортогонална квадратна матрица (или в случая на единична матрица Hermitian пространство) и verhnetreugolnoymatritsy с положителни диагонални елементи, който е специален случай Iwasawa разлагане.

Смята се, b1 = a1. и ако векторите, които вече са построени

Геометричната смисъла на описания метод се състои в това, че при всяка стъпка на вектор би yavlyaetsyaperpendikulyarom възстановен до линеен участък на векторите на крайния vektoraai.

Нормализиране получени вектори Bi,

получите желания ортонормален CI> система.