Плавно голяма функция 1
Определение. F функцията (х) е безкрайно по-голям от х → x0. т.е.. ако по някаква съществува такова, че за всички по-- квартала.
- Ако това е важно да се отбележи знака на една безкрайно големи функции, + или пишете на символа. Например,
Забележка Constant не е безкрайно малко, без значение колко малък е той може да бъде. Само броят 0 може да се разглежда като безкрайно.
Забележка Не можете да извикате функция или една безкрайно голяма или безкрайно малко, ако не е посочено квартал на мястото, където той се лекува.
Така че, ние видяхме, че функцията е безкрайно като х → ∞ за безкрайно голям х → 2
Комуникацията между безкрайно големи и безкрайно малки функции, като теорема, изразени от:
Теорема. Ако има безкрайно малко, в района на х = x0 .. функцията е безкрайно голяма в съседство с една и съща точка.
Ние формулираме няколко теореми на безкрайно малки функции.
Теорема. Алгебрични сумата от краен брой безкрайно функции в съседство с х = x0 е безкрайно функция в съседство на х = x0.
Теорема 4.4. Работната функцията на безкрайно малко в близост до х = x0 да функционира в ограничен квартал на х = x0. безкрайно функция в съседство на х = x0.
Следствие 1. Произведение безкрайно функция в околност на х = x0 с постоянна стойност е функция на безкрайно малко в близост до х = x0.
Следствие 2. произведение на две безкрайно малки функции okrestnostitochki х = x0. безкрайно функция в съседство на х = x0.
По този начин, сума, разликата и продукта от краен брой безкрайно функции в близост до х = x0 безкрайно в непосредствена близост до една и съща точка.
Това не може да се каже и за отношението им. Например, ако х → 0. След това те са безкрайно малък в близост до х = 0. и връзката им като х → 0:
От това следва, че отношението на две безкрайно малки функции в близост до х = x0 е несигурността от типа
Съотношението на две безкрайно големи функции е също несигурност, която е обозначена с
За изчисляване на границата на отношението на две безкрайно малки или безкрайно големи две функции, е необходимо извършването на допълнителни изследвания, които се наричат неопределен тип форма, съответно, и с тях ще научим по-нататък.
Теорема. Ако F функция (х) има горна граница е равна А. може да бъде представен като сума от броя А малки функции ibeskonechno # 945; (х). т.е. ако
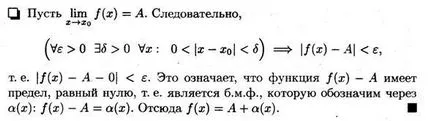
Теорема (обратна). Ако F функция (X) може да бъде представена като сумата от А и безкрайно функция # 945; (х), номер А е границата на F функция (х). т.
напр. ако е (х) = A + # 945; (х), след това

Теореми за граници
За да се изчисли границите необходими, за да използвате някои правила. Тези правила са формулирани под формата на теореми, които ние формулираме по-долу. За да се въвеждат тези теореми, като се използва следната теорема:
Теорема. За функция у = е (х) при х = x1 имат граница брой необходимо и достатъчно, че тя е представена в близост до дадена точка като сума,
при което - безкрайно функция в съседство на х = x1.
Теорема. Якост алгебрична сума (разлика) на определен брой функции, които имат ограничение в точка х = x0. равна на сума (разлика) отношение на ограниченията за:
Доказателство. Нека тогава, от теоремата на функцията за връзка, нейната граница и b.m.v. може да се запише: и следователно
Следствие функция може да има само една граница, когато х → x1
Теорема. Опън работи определен брой функции, които са извън точка х = x1. равна на произведението от границите на фактора:
Следствие. Постоянен коефициент може да се приема като знак на срока:
Следствие. Limit степен с естествен показател е една и съща граница степен:
. по-специално. пÎN
Теорема. Ако функция у = F (х) има точка х = граница на x1 е различно от нула, тогава функцията - е ограничено в близост до дадена точка.
Теорема. Границата на частното на две функции, имащи граници, равен на съотношението на граници на тези функции, при условие, че границата на знаменател не е нула:
Ние се формулира критерий за съществуването на граници:
Теорема. Ако се установи стойността на F функция (х) между съответните стойности на Е1 функции (х) и f2 (х). които са склонни да се ограничи и един по х = x1. след това е (х) при х = x1 също има лимит номер. т.е. ако