Парабола и нейното канонично уравнение

Най-накрая! Тя е най-много. Готови ли сте да разкрие много тайни. В каноничен уравнение има формата на парабола. където - действителният брой. Лесно е да се забележи, че в своето нормално положение парабола "лежи на едната си страна" и неговия връх е в основата. Функцията определя горния клон на линията, както и функцията - долния клон. Очевидно е, че параболата е симетричен около оста. Всъщност, това, което се извиси:

Решение. върхът е известно, ще намерите допълнителни точки. Уравнението определя горната дъга на уравнение на парабола - долната дъга.

С цел намаляване на изчисляването рекорд ще прекарат "под един гребен":

За компактен запис могат да се подреждат резултати.

Преди да извършите лесен Pointwise рисунка, формулира строг

Парабола е множеството от всички точки в равнината на еднакво разстояние от дадена точка и дадена линия. не минава оттам.

Точката се нарича фокусна точка на параболата, прав - директорка (лимец с един "ес") парабола. Постоянно "PE" каноничен уравнение се нарича фокусно параметър. което е равно на разстоянието от фокуса на направляващата. В този случай. По този начин във фокуса има координати. и директорка дава с уравнението.
В нашия пример:

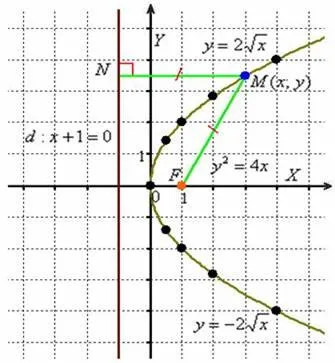
Определяне парабола разбрано още по-лесно, отколкото определянето на елипсата и хипербола. За всяка точка от параболата на дължината на сегмента (разстоянието от фокуса до точка) е равна на дължината на перпендикуляра (разстоянието от точката на направляващата):

Честито! Много от вас са направили днес е истинско откритие. Оказва се, хипербола и парабола, не са на всички класации "обикновените" функции и имат ясно изразен геометрична произход.

Очевидно е, че ще се "чува" нагоре и надолу, доближавайки безкрайно близко до оста с увеличаване на фокусна параметър генериран клон. Когато намаляването на същите ценности "PE", те започват да се компресира и се простира по протежение на оста

Изместването на всяка парабола е равен на една: