Означаваме проекции върху координатните оси, чрез

Получават - тази формула е основният вектор и изчисляване nazyvaetsyaRazlozhenie вектора на единичен вектор на координатните оси. численост

nazyvayutsyakoordinatami вектор.

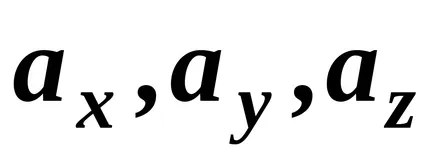
Проекциите на вектора на координатните оси се наричат ​​неговите координати. Това е тяхната геометрична значение.

Уравнението на вектор понякога се пише в символична форма

.

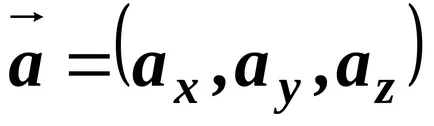
Познаването на вектор проекцията може лесно да се намери дължината му, т.е. модул. Въз основа на теоремата от дължината на полето по диагонал.

Т.е. единичен вектор е корен квадратен от сумата от квадратите на прогнози си върху осите. координати.

Нека векторните ъгли с координатните оси съответно

. Според прогнозите на имота да има оста. (*)

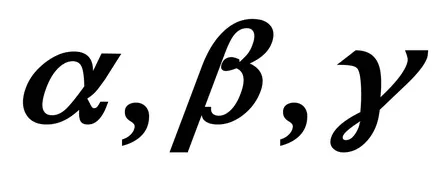
Opr.12Kosinusy ъгли, който образува вектор от координатните оси, nazyvayutsyanapravlyayuschimi kosinusamivektora.

Ако векторът е дадена в равнина, а след това.

Те имат забележителен имот:

.

От формули (*) означава, че координатите на единичен вектор са уюта на посока, т.е. ,

5. Действия на вектори в компонент форма

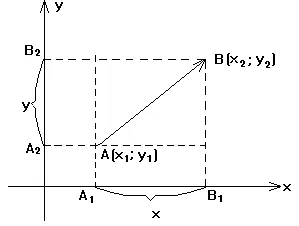
За всяка точка в DSC координати на ОМ-радиус-вектора са координатите

Ако в началото на вектора не съвпада с произхода, но известни координатите на началната и крайна точка А Б, координатите на вектора

Те представляват разликите от подобни координати на нейните начални и крайни точки.

.

Това двумерен пространство (R 2).

По същия начин, в триизмерното пространство. ако

,, на

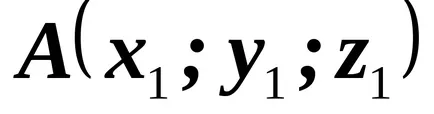
Ако известните координати на вектора

, след това си величина е равен на корен квадратен от сумата от квадратите на координатите.

.

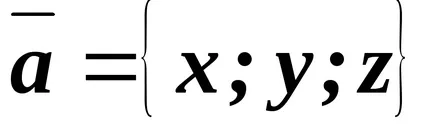
уюта посоката на всеки вектор се изчисляват чрез следните формули:

.

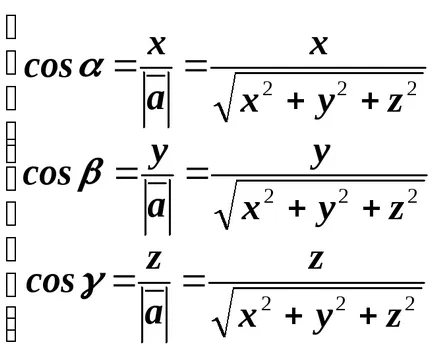
Ако векторите

илежат на една права, тогава съответните координати на своя пропорционален:.

Обратното е вярно, т.е. ако връзката г.

.

§3. N- двумерен вектор пространство. Линейна зависимост и независимост на вектори.

N - двумерен вектор пространство.

2. линейна зависимост и независимост на вектори

3. В основата на пространството за вектор. Разширяване на вектора в базата

1.N- двумерен вектор пространство

Да предположим, че имаме система

вектори:

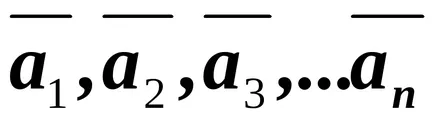
тип Opr.13 .Vyrazhenie :, (3.1) където

-реални числа, nazyvaetsyalineynoy

Opr.14.Sistema вектори

nazyvaetsyalineynonezavisimoy ако линейна комбинация на (3.1) е равна на нула, при условие, че всички = 0, т.е. , (3.2)

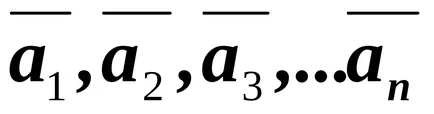
Ако линейна комбинация на (3.1) е равна на нула, при условие, че поне един от номерата

, системата от вектори (3.1) nazyvaetsyalineyno зависими.

Ако системата съдържа повече от един вектор

, линейната връзка, това означава, че най-малко един от векторите на системата може да бъде представена като линейна комбинация от други векторни системи. Всъщност, предполагам, че векторителинейно зависими и нека. След това можем да разделим двете страни в (3.2) доекспресиращ векторчрез други вектори; т.е. представи това като линейна комбинация:

.

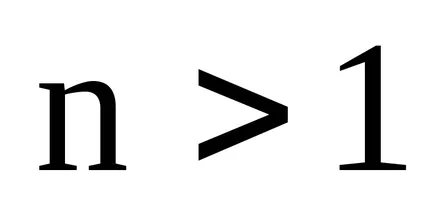
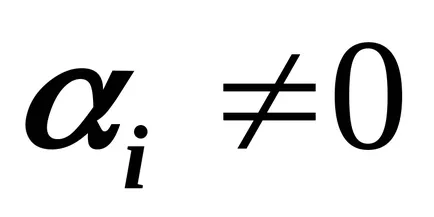
Ако всички членове на (3.3), за да се движат на една страна, ние откриваме, че линейна комбинация е равна на нула, при условие, че коефициентът на вектора

Тя е различна от нула. Тя е равна на (-1).

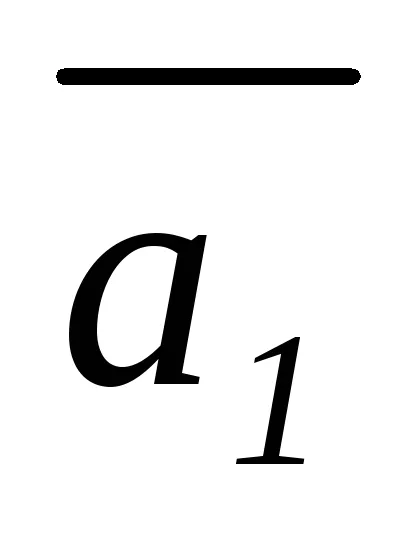
Vyvod.Esli най-малко един от векторите е линейна комбинация (т.е., изразена по отношение на другия), след това цялата система на вектори е линейно зависим. Необходими и достатъчни условия за линейна зависимост на двата вектора на равнина (в prostranstveR2) е тяхната колинеарност, и в триизмерното пространство (R3) - им една равнина.

Системата се състои от вектор (R 1 пространство) е линейно зависим, ако векторът е нула, и ако е различен от нула - това е линейно независими.

В пространството

(В линия) са линейно независими система не може да съдържа повече от един вектор, т.е. Система от две (или повече) вектори са винаги линейно зависими.

В пространството

(В равнината) линейно независими система не може да съдържа повече от два вектора, т.е. Всяка система от три (или повече) вектори е линейно зависим.

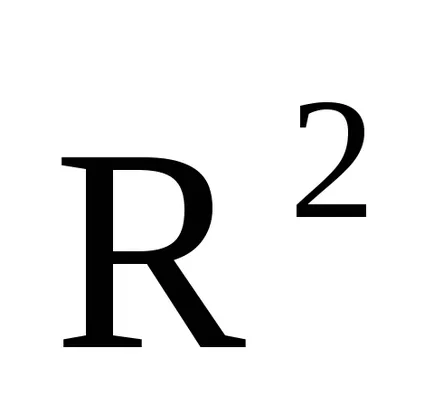
Ако има линейна пространство

линейно независими вектори, и всекивектори са линейно зависими, след което пространството се нарича ограничен двумерен ако линеен пространство, така че съществува система на произволно голям брой линейно независими вектори, това пространство се нарича безкраен.

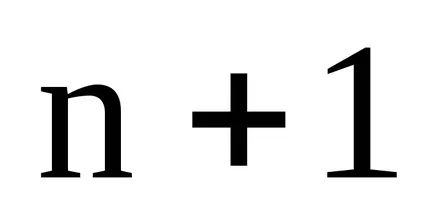
Максималният възможен брой линейно независими вектори в краен тримерно пространство е измерение на това място. Ако измерение на пространството е

, той се нарича- измерна ().

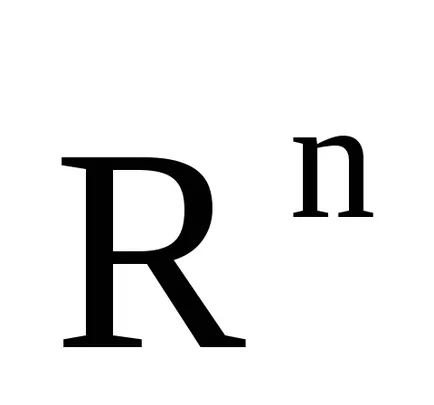
Opr.15.Sistema

линейно независими вектори- тримерно пространство nazyvaetsyabazisometogo пространство.

базисни вектори могат да се разделят на всеки вектор пространство, с по уникален начин.

Разлагане на векторни базисни вектори - е да се представи като линейна комбинация на векторите на тази основа.

Ако основата е

линейно независими вектори, след разширяването на всеки векторВъз основа на това е както следва :. (3.4)

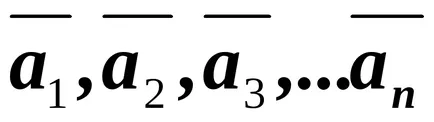
Коефициентите на това разширяване, т.е. номер вектор nazyvayutsyakoordinatami

в тази база.

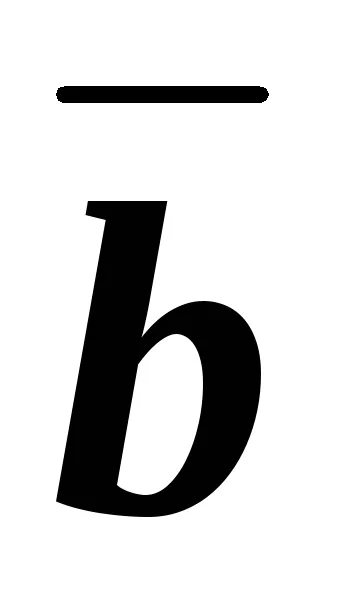
За да намерите тези номера трябва да се създаде система

- линейни уравнения с тези неизвестни, и да го решим.

Всяка уравнение се състои от формула (3-3) от съответните координати на тези вектори.

Пример примера векторите:

;;;.

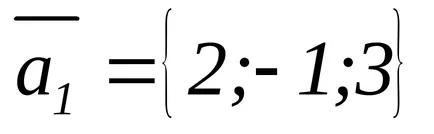
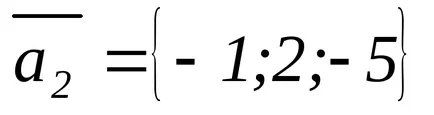
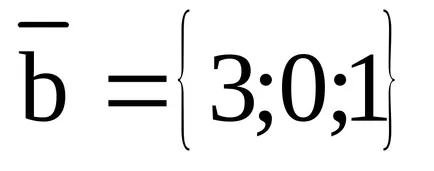
Покажете, че векторите

разлагат и образуват основа векторна тази основа.

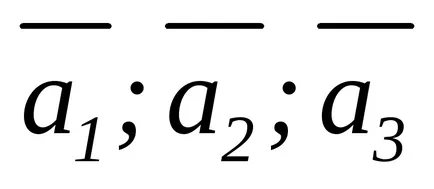
Решение. вектори

представлява основа на триизмерното пространство, ако те са линейно независими, така че трябва да се направи определящ фактор за координатите на тези вектори. Ако е нула, неговата ред (и следователно на векторите) са линейно зависими, т.е. те не могат да образуват основа, ако детерминантата не е нула, векторите са линейно независими и образуване на основа.

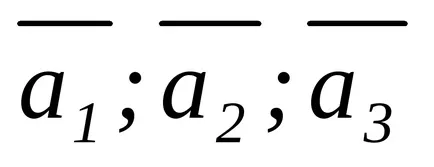
разложен вектор

въз основа- това означава да го представи като линейна комбинация от тези вектори:

. (*)

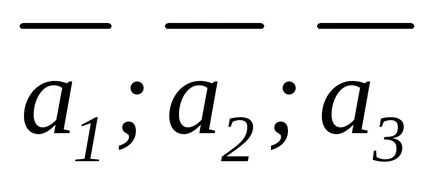
Тъй като вектор на базисни вектори, получени от формула (*), след което всеки от своя координира се получава от съответните координати на тези вектори в същата формула (*).