Основни закони на магнитно поле

Както и всяка друга векторно поле, полето може да бъде представляван от векторни линии. Те се извършва по конвенционален начин - така, че допирателната към тези линии във всяка точка съвпада с посоката на вектора. и плътността на линиите ще бъде пропорционална на големината на дадена точка от пространството.

1). теорема на Гаус в поле. поток на магнитната индукция чрез всяка затворена повърхност е нула:

Т.е. векторни линии нямат никаква начало и край. Поради това броят на векторни линии. излъчвана от всеки обем, ограничена от затворената повърхност S. Той винаги е равен на броя на линиите, включени в този том.

Гаус теорема, както и че в природата не съществуват магнитни заряди, които биха началото или в края на вектора на линия, т.е. магнитно поле не разполага с източници, за разлика от електрическо поле.

В диференциална форма Гаус теоремата за областта е на формата

Различие polyavsyudu нула. Този закон е валидно не само за устойчиви, но също така и за променлив магнитни полета.

2). Теорема на Circulation вектор (за магнитното поле постоянни токове във вакуум).

Циркулацията на вектора на магнитната индукция по произволен затворен път е равна на произведението на магнитната константа алгебрични сумата от течения, обхванати от верига:

Текущ се счита за положителен, ако посоката й се дължи на посоката на пресичане на контура на върховенството на десния винт.

Ако текущата I се разпределя по обем, тя може да бъде представен като. където S - произволна повърхност калибрира чрез линия L.

Vector образува и байпас с посоката на десняк система.

От обращение теорема следва, че магнитното поле не е потенциален (за разлика от електростатичен). Такава област се нарича завихряне или соленоидни.

Теорема на циркулацията на вектора прави много по-лесно, отколкото на Био - законът Savart за изчисляване на магнитното поле в някои симетрични системи.

В диференциална форма теорема циркулация вектор има формата:

вектор ротор магнитно поле е продукт на магнитната индукция при постоянна електрически ток плътност дадена точка в пространството.

Прилагане на вектор циркулация теорема

Нека ток, преминаващ по протежение на безкрайно дълга права тел с кръгло напречно сечение, с радиус R.

2). Магнитното поле на бобината, през която тече Токио:

Нека за единица дължина на соленоида трябва да п навивки на проводника.

Ако стъпка спирала е достатъчно малка, че всеки ход на намотка може да бъде приблизително заменя с затворена кръгова намотка. Ние също така се предположи, че секцията диригент е толкова малка, че токът може да се разглежда като протичащ по повърхността.

Опитът показва, че за достатъчно дълги соленоида магнитното поле извън соленоида близо до нейната повърхност е почти нула.

От съображения симетрия е ясно, че във вътрешността на електромагнитни векторни линии са насочени по оста си.

Избор на правоъгълен контур (пунктирана линия на фигура показва) със страна л. разположени успоредно на оста соленоид.

От теоремата на циркулацията,

където броят на ампернавивките.

От съображения за симетрия следва, че векторни линии трябва да са кръгове, чиито центрове са разположени на OO ос ".

Както верига изберете една от тези кръгове.

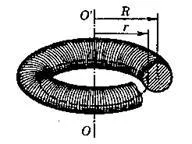
Нека N - броят на навивките в тороида;

I - ток във всеки цикъл:

От теоремата на циркулация вътре в тороида.

Извън тороида. т.е. магнитното поле не е налице.

При сегашните проводници в магнитното поле

Всеки текущата превозвач изпитва магнитна сила. Действието на тази сила се предава на проводника, по които се движат обвиненията. В резултат на това магнитното поле действа с особено сила на проводник с ток.

обемна плътност на електрически заряд;

елемент диригент Малък обем;

скорост на движение нареди на обвиненията.

Ако токът тече през тънката жица, а след това ние получаваме право на Ампер

Силата на взаимодействие между две успоредни проводници tokamiI1 II2. които са на rasstoyaniib друг.

Текущ I1 създава около себе си магнитна индукция област.

За единица дължина на проводник със сила ток I2.

Токовете същата посока привличат и противоположно насочено - отблъсне.