Опростяване на логически изрази
Еквивалентно преобразуване логически формули имат същата функция като формули за превръщане в нормална алгебра. Те служат за опростяване на формулите, или да ги доведе до определена форма чрез използването на основните закони на алгебрата на логиката.
Съгласно формула реализират еквивалент опростяване преобразуване, в резултат на формула, която не съдържа нито един от операции Последици и стриктно еквивалентност дизюнкцията или съдържа в сравнение с първоначалната минимален брой операции на връзка, дизюнкция и инверсии или съдържа минимален брой променливи.
Някои трансформации на логически формули, подобни на формулите за преобразуване в обичайната алгебра (налагането на общ фактор от скобите, използвайте комутативен и асоциативни законите, и т.н.), докато други се основават на превръщането на имоти не обладани от обикновените операции на алгебрата (с помощта на разпределителни закона за съюзи законите на абсорбция, залепване, де Morgan и др.).
Ние показваме някои примери в техниките и методите, използвани при опростяването логически формули.
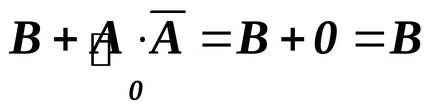
В този пример се прилага законите противоречие (11) и константи изключване (7).
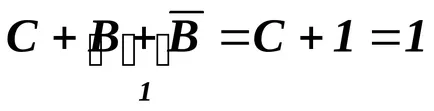
В този пример, приложен принципа на противоречие (11) и операцията определение "логически добавянето" на.
В пример 3 Прилагане на практика на противоречие (11) и константи изключване (7).
В примера (4) се прилага законодателството на противоречие (11) и операцията по дефиниция "на AND".
Логическите закони се прилагат в този пример в следната последователност: правило DeMorgan на (14), асоциативно закона (6), правото на противоречие (11) и операциите по правило с константи (7).
Логическите закони в този пример се използва в този ред: върховенството на де Морган (14) се изважда от скобите общ фактор (разпределителни право (8)), правото на противоречие (11).
В този пример, негативите за nonelementary формули правило важи De Morgan ((14) и (15)); асоциативен право (6) са използвани закони двойно отрицателни (13) и операцията по дефиниция "логично допълнение".
Често, за да се опрости булеви изрази се прилагат следните самоличността:
Използването на тези формули означава, че всеки израз може да бъде умножена по единица или добавите думи на нула. например:
Тези примери показват, че опростяването на логически формули не винаги е очевидно, което на законодателствата на алгебра на логиката трябва да се прилага по-специално стъпка. Умения идват с опит.
Изграждането на функциите на логиката на базата на математически изрази
Логически функции често се формират на базата на математически изрази. Математическият израз е известно, че съдържа променливи, константи и функции, свързани с признаци на математически операции. Но за да се създаде функция логика изисква да използват релационни оператори: <,>, ≤, ≥ =, ≠. В резултат на който и да е от тези операции е "вярно" или "невярно", който ще означаваме 1 или 0. По този начин, всяка операция отношения създава едно просто твърдение.
Например, изразът X> Y е 0 или 1, в зависимост от конкретните стойности на X и Y. По този начин е възможно да се образуват логика функция е на реални променливи X и Y, които ще бъдат вярно, ако условието дефинирани по-горе. Писано е по този начин:
Друг пример. Форма функция логика, която ще бъде вярно, ако променливите х и у са кратни на три; х, у-целочислени променливи.
Решение. Имайте предвид, че е цяло число и е кратно на цяло число, б. ако остатъка от деление число на от б е нула:
Тук мод операция запис означава изчисляване на остатък при целочислено деление на по б.
Условията на проблема е лесно да се идентифицират две прости твърдения: х е кратно на три и у е кратно на три. Между тези отчети трябва думата "и". Поради това е трудна задача съдържа логически умножение и математически това твърдение може да се запише като:
Помислете още един пример. Форма функция логика, която ще бъде вярно, ако сумата на и B- положителен, докато стойността на или B- отрицателна. и B- недвижими тип променливи.
Решение. В този пример, също могат да бъдат идентифицирани няколко прости твърдения:
а- стойност е отрицателна;
Първият цитат е свързан с два други съюз "а", което означава, че между логическото умножение. Освен това, вторият и третият прости твърдения, свързани с "или", което означава между логическа операция допълнение. По този начин, ние получаваме следната функция:
В скобите в този израз променят реда на операциите. Това е необходимо, тъй като операторите за отношения имат най-нисък приоритет.
Друг клас операции отношения, свързани с координиране на самолета. Нека дам един прост пример, за да образуват функция логика, която ще бъде вярно, ако точката принадлежи на защрихованата област (виж Фигура 1.).
Решение. Според фигурата, въпросът трябва да бъде в кръга на радиус 1 с една ръка, а от друга - да бъде в горната половина. Уравнението на окръжност с радиус 1 има формата:
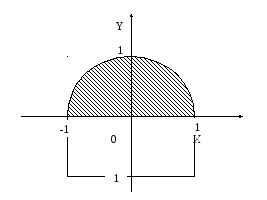
където X и Y - координати на точки, принадлежащи на кръга. Въпросът е в кръга, ако нейните координати удовлетворяват следното условие:
Към точка в горната половина е необходимо условие Y ≥ 0. Тези две условия трябва да бъдат изпълнени едновременно, което е възможно само за логическо умножение. Следователно, необходимо е функция на формата: