област полигон

Можем да кажем, че площта на многоъгълник - стойност, показваща част на самолета заета от многоъгълника. Per измерване единица площ, като квадратна зона с страна \ (1 \) cm \ (1 \) мм и т.н. (Единица квадрат). Тогава областта ще се измерва в cm \ (^ 2 \). mm \ (^ 2 \), съответно.

С други думи, можем да кажем, че площта на фигурата - е стойността, цифровата стойност, която показва колко пъти площад единица се вписва в тази цифра.

1. Площта на всеки полигон - положителна стойност.

2. Равни полигони имат равни части.

3. Ако полигон състои от няколко полигони, площта на повърхността е равна на сумата от площите на тези полигони.

4. Площта на квадрат със страна \ (а \) е \ (а ^ 2 \).

Теорема: площ на правоъгълник

Площта на правоъгълник със страни \ (а \) и \ (б \) е равна на \ (S = аб \).

Завършване на правоъгълник \ (ABCD \) на квадрата на \ (а + б \). както е показано по-долу:

Този площад е правоъгълник на \ (ABCD \). друг, равен на него правоъгълник и два квадрата със страни \ (а \) и \ (б \). По този начин,

Ръст успоредник - перпендикулярна съставен от върха към страната на успоредник (или да продължат страна) не съдържат този връх.
Така например, на височината на \ (BK \) се пада на страна \ (AD \). а височината \ (BH \) - продължаване на страните \ (CD \):

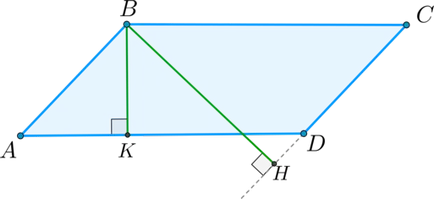
Теорема: областта на успоредник

Площта на успоредник е равна на произведението на височината на страните, до които се осъществява тази височина навън.

Начертайте вертикалите \ (AB '\) и \ (DC' \). както е показано на фигурата. Имайте предвид, че тези вертикалите са равни на височината на успоредник \ (ABCD \).

Тогава \ (AB'C'D \) - правоъгълник, следователно, \ (s_ = AB '\ cdot AD \).

Имайте предвид, че на правоъгълни триъгълници \ (ABB '\) и (DCC \' \) са равни. По този начин,

Ще се обадим на страната, към която триъгълника проведе височината на триъгълник база.

Площта на триъгълник е равен на половината от произведението на основата му и височината, извършена от тази фондация.

Нека \ (S \) - триъгълник площад \ (ABC \). Ние се по посока на \ (AB \) от основата на триъгълника и привлече височина \ (CH \). Ние показваме, че \ покритие триъгълник \ (ABC \) на успоредник \ (ABDC \), както е показано по-долу [S = \ dfracAB \ cdot СН \.]:

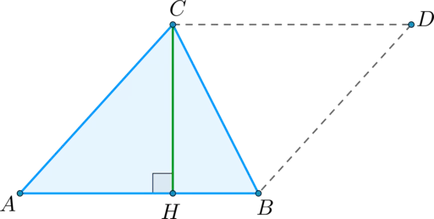
Триъгълниците \ (ABC \) и \ (DCB \) са от три страни (\ (Британска Колумбия \) - общата им страна, \ (AB = CD \) и \ (AC = BD \), тъй като другата страна на успоредник \ (ABDC \ )), така че техните райони са равни. Ето защо, област \ (S \) триъгълник \ (ABC \) е равен на половината от площта на успоредник \ (ABDC \). т.е. \ (S = \ dfracAB \ cdot СН \).

Ако два триъгълника \ (\ триъгълник ABC \) и \ (\ триъгълник A_1B_1C_1 \) има същата височина, тяхната област на загриженост като база, до която прави от надморската височина.

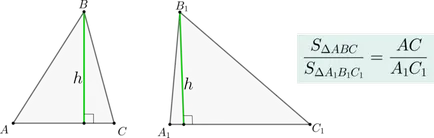
Медианата на триъгълник го разделя на два триъгълника с еднаква площ.

Ако два триъгълника \ (\ триъгълник ABC \) и \ (\ триъгълник A_2B_2C_2 \) всеки има равни права, те са като работна площ на страните, които формират ъгъл.

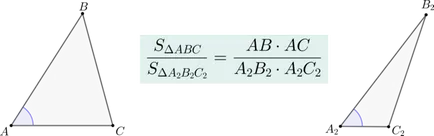
Нека \ (\ ъгъл А = \ ъгъл A_2 \). Съвместими тези ъгли, както е показано (точка \ (А \) е подравнен с точка \ (A_2 \)):

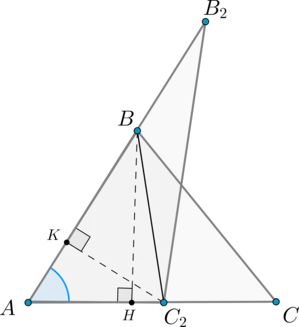
Начертайте височина \ (BH \) и \ (C_2K \).

Триъгълниците \ (AB_2C_2 \) и \ (ABC_2 \) имат една и съща височина \ (C_2K \). Следователно: \ [\ dfrac >> = \ dfrac \]

Триъгълниците \ (ABC_2 \) и \ (ABC \) има същата височина \ (BH \). Следователно: \ [\ dfrac >> = \ dfrac \]

квадратен правоъгълен триъгълник хипотенузата на дължина, равна на сбора от квадратите на дължините на краката:

Обратно, ако триъгълник квадрат дължина на едната страна, равна на сбора от квадратите на дължините на другите две страни, правоъгълен триъгълник.

Площта на правоъгълен триъгълник е равен на половината от работата на крака.

Теорема: Формула чапла

Нека \ (р \) - триъгълник semiperimeter, \ (а \). \ (B \). \ (С \) - дължината на своите страни, а площта му е \ [S _ = \ SQRT \]

защото ромб е успоредник, това е вярно, същата формула за това, т.е. област ромб е равно на произведението на височината на страните, до които се осъществява тази височина навън.

Площта на изпъкнал четириъгълник, диагонала, която е перпендикулярна, равна на половината от продукта на диагоналите.

Помислете за четириъгълник \ (ABCD \). Нека \ (AO = а, CO = б, BO = х, DO = Y \):

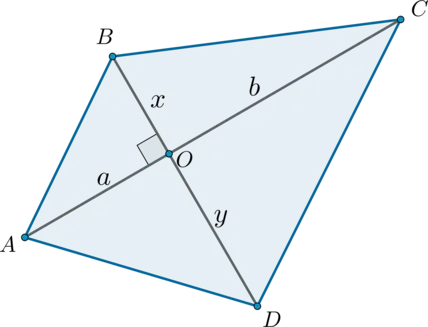
Имайте предвид, че този правоъгълник се състои от четири правоъгълен триъгълник, следователно, с площ, равна на сбора от лицата на триъгълници:

\ (\ Започнете S _ = \ frac12ax + \ frac12xb + \ frac12by + \ frac12ay = \ frac12 (брадва + Хб + с + AY) = \\ \ frac12 ((А + В) х + (А + В) у) = \ frac12 (а + б) (х + у) \ край \)

Въздействие: Площта на ромб

Площта на ромба е равна на половината от продукта на диагоналите: \ [S _> = \ dfrac12 d_1 \ cdot D_2 \]

Височината на трапеца - перпендикулярно от върха на една база в друга база.

Теорема: района на трапеца

Площта на трапец е равна на произведението на половин сумата от бази на високо.

Помислете трапец \ (ABCD \) с бази \ (BC \) и \ (AD \). Начертайте \ (CD '\ успоредно AB \). както е показано по-долу:

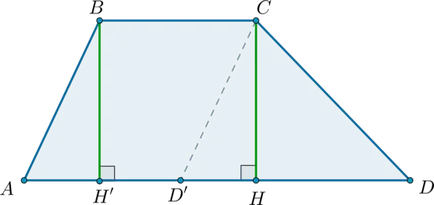
Тогава \ (ABCD '\) - успоредник.

Draw като \ (BH '\ престъпника АД, CH \ престъпника AD \) (\ (BH "= CH \) - височината на трапеца).

Тогава \ (s_ = BH '\ cdot АД "= BH' \ cdot пр.Хр., \ четириядрен S _ = \ dfrac12CH \ cdot D'D \)

защото трапец се състои от успоредник \ (ABCD '\) и триъгълник \ (CDD' \). че неговата площ е равна на сумата от лицата на успоредник и триъгълник, който е:

\ [S_ = s_ + s_ = BH '\ cdot BC + \ dfrac12CH \ cdot D'D = \ dfrac12CH \ наляво (2Вс + D'D \ дясно) = \] \ [= \ dfrac12 СН \ наляво (Британска Колумбия + AD " + D'D \ дясно) = \ dfrac12 СН \ наляво (Британска Колумбия + AD \ дясно) \]