Нормално разпределение, Гаусово разпределение
Това разпределение е в центъра на теорията и практиката на вероятностни и статистически анализи. Нека ценностите на разследван непрекъсната случайна променлива са повлияни от много голям брой независими случайни фактори, устойчивостта на удар на всеки отделен фактор е малък и не може да надделее сред другите, и естеството на въздействието - добавка.
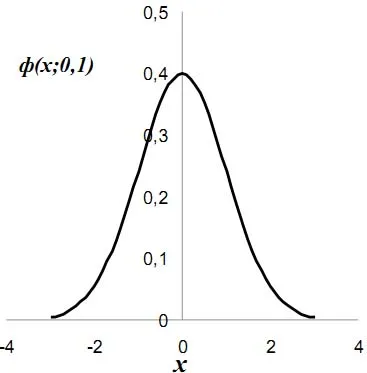
Плътност функция на случайни променливи от този тип е, както следва:
където ц и σ 2 право параметри се интерпретират като очакването (средна стойност) и разсейването на случайна променлива.
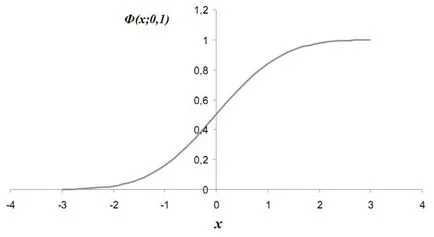
Съответната функция на разпределение на нормална случайна променлива
Нормално закон с функция плътност
(Μ = 0 и σ 2 = 1) се нарича стандарт. В много случайни величини изучавани в областта на икономиката, инженеринг, биология, както и други области, разбира се види общата добавка ефекта на голям брой независими причини.
Концепцията за нормално разпределение
Нормално закон - е един от многото видове разпределителни налични в природата, но с относително голяма част от практическо приложение. Пълнота на теоретични изследвания, които се отнасят към нормалния закона, както и относително прости математически свойства го правят най-атрактивната и лесна за използване.
В случай на отклонение от тестовите експериментални данни на нормален закон, има най-малко два начина за правилната употреба на лекарството: а) да го използва като първо приближение; Често се оказва, че това предположение дава достатъчно точни по отношение на специфичните цели на резултатите от проучването; б) избор на преобразуване разследван случайна променлива, която променя оригиналния "не е нормално" закона разпределение, превръщайки го в един нормален.
Удобен за статистически проблеми и е собственост на "samovosproizvodimosti" нормална държава, състояща се в това, че сумата на произволен брой нормално разпределени случайни величини също подлежи на нормален закон за разпределение.