нискочестотен филтър
.
В пропускане, т.е. на интервала от 0 до
квадратен Chebyshev полином ще варира в интервала [0, 1], алтернативно, като екстремните стойности на (N + 1) пъти. Функцията и разглеждания честотен интервал ще получи същия брой пъти стойностите [0; 916 #; а].
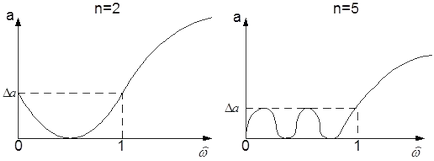
Фигура 6 показва графики на затихване Chebyshev полином LPF за стойностите п = 2 и п = 5 за идентичен # 916 а.
функционални тестове и (
) Позволява ви да извършвате редица важни и интересни изводи за практиката:
1. С една и съща стойност на # 916, и увеличаване на реда на предавателната функция увеличава стръмнината на характеристиките на затихване извън пропускане.
2. С постоянна стойност на затихване н честотна лента е по-голяма, толкова по-голям # 916 а.
3. Най-малката (равно на 0) и най-високата (равен # 916; а) намаляване стойности алтернативен в пропускане. "Покупки с равен" Ето защо сближаването Chebyshev често се нарича.
4. затихване на филтъра при ареста на банда с увеличаване на честотата нараства монотонно.
Според зададени изискванията за характеристика затихването в stopband за Chebyshev нискочестотен филтър се изчислява по същия начин както за Butterworth нискочестотен филтър, като се излиза от състояние (
)
Решаването на този неравенство за п получаваме:
Изграждане на функция Т (р) е известен | T (к
) | 2 се получава по обичайния начин. стълба изпълнение на схемата ще има същата форма като тази на всеки друг полином нискочестотен филтър със същия п.
Разликата е само в стойностите на стойностите на параметрите на елементите. Дадените в таблица решения за изчисляване на Chebyshev LPF дадено в справочна литература.
Chebyshev филтър има предимството, че еднакъв брой елементи и в същото време, # 916: и лентовата, филтърът има по-голям затихване в stopband спрямо Butterworth филтър.
3. LPF с затихване поредици (е-RY Zolotareva)
Отличителна черта на характеристиките на затихване на LPF е полином на монотонна увеличение с увеличаване на разстоянието от пропускане. Все пак, ако искате да се синтезира LPF с високо ниво на гарантирана затихване a0 и тесен преход банда, използването на полином структури води до неоправдано голям брой елементи в такива случаи, че има смисъл да се обърнат към други трансферни функции, по-специално, има нули, и лента за задържане пръски гниене, т.е. функции на формата:
- Hurwitz полином от степен п;
- лента задържане честота където честотната характеристика на филтъра става нула (затихване става безкрайно голяма, т.е. притежава своя "взрив").
честота зависимостта на затихване е:
Сред филтър нискочестотен, чиято функция прехвърляне има форма фракция (5), най-широко използван нискочестотен филтър с характеристики на затихване izoekstremalnymi Zolotaryova или LPF.
Изисквания за затихване характеристика на LPF от този тип се приготвят както следва: затихването в пропускане на филтъра не трябва да надвишава предварително определена стойност # 916 А, ленти задържане да бъде не по-малко от a0 предварително определена стойност.
В такива случаи приближение филтър с характеристиките на отслабване на задачите, с помощта на един от най-добрите функции сближаване формулирана и решен EI Zolotarev (1847-1878), професор в университета в Санкт Петербург, ученик PL Chebyshev, а именно проблема на рационална функция за п, стойностите на която абсолютната стойност в диапазона от -1
1 не може да е повече от един, а в интервала |
|> 1-малката в абсолютна стойност, стойността му ще бъде възможно най-доброто.
Подходящ рационална функция може да се нарече Zolotaryova дроб.
Ако експресия = 10lg (1 + А0 PN 2 (
) Позиция Zolotaryova разбира, в съответствие със свойствата на крайната стойност на най-малкия затихване на филтъра в групата на задържане е най-високото възможно в сравнение с всички други филтри с еднакви стойности.
График LPF Zolotaryova затихване характеристики, а също така е възможно прилагането верига са показани за случая на п = 5 на фигура 7.

Вижда се, че шиповете на затихване са подредени така, че минималната стойност в лентата на задържане са еднакви и равни.
Филтри с характеристики Zolotaryova (или просто Zolotaryova LPF) понякога се нарича елиптична, тъй като стойностите на нули и полюси Zolotaryova фракция изразени по отношение на елиптичните функции.
Решенията, свързани с изчисление LPF Zolotaryova момента таблични и доведени до веригите и елемент стойности на параметри (вж. L.2, стр. 292-295).
Ефикасността Zolotaryova LPF може да се потвърди чрез пример, където нискочестотен филтър налага скоро строги изисквания.
Изчисление на наш ред различни филтри, които отговарят на горепосочените изисквания ще доведат до:
Броят на елементите равна на, съответно, 7, 18, 80.
В този пример, LPF Zolotarev е ясно от конкуренцията.
Детайлно изследване на свойствата на различни филтри може да се заключи, че в някои конкретни случаи със сравнително широки преходни ленти минимален брой елементи могат да имат полином LPF. Може да има ситуации, в които броят на елементите Zolotaryova LPF и LPF Chebyshev полином са идентични. След това се отдава предпочитание на един тип, който е по-пълно отговаря на другите изисквания (размер, технология на производство и т.н.).
Литература се използва за подготовка на лекции
1. AF Beletsky "Теорията на линейни електрически вериги" София 1986 в 368-395
Всички материали в "Телеком"