Ние се подготвяме за изпита по математика

За решаването на проблеми (С2) започва след повтаряне на "перпендикулярни линии и равнини", "polytopes".

Базова линия четириъгълна призма ABCDA1 В1 С1 D1 - правоъгълник ABCD, където AV = 5, AD =. Виж допирателната на ъгъла между лицата равнина на призма АА1 D1 D и равнината, минаваща през центъра на диска ръбове перпендикулярна линия В1 D, ако разстоянието между правите линии А1 и С1 равни на BD.

Ние намираме косинуса на ъгъла между тези самолети, като модул на косинуса на ъгъла между нормалите на тези самолети. Вектор AB - перпендикулярна на равнината на лицето АА1 D1 г, вектор DB1 - нормално в различна равнина.
Представяме координатната система и да се определят координатите на точките А (5, 0, 0), В (0, 0, 0), D (5 ,; 0), В1 (0, 0)

Ъгълът между тези равнини могат да бъдат определени като ъгълът между правите линии, перпендикулярна на самолети, и тази директна DC В1 D.

С триъгълник BB1 находка B1 C:

От B1 DC триъгълник намираме тангенса на ъгъла B1 DC

След анализ на решението на проблемите на студентите се изисква да направите избор на задачите от изпита материали, за да ги решим по различни начини и да се говори за съучениците си по време на конференцията. В резултат на индивидуална и групова работа е представен

Решение на проблеми, свързани с параметрите

S5.Nayti всички стойности на един, така че уравнението има уникално решение.

Помислете за функцията.
Ако се увеличава.

Следователно най-малката стойност на F функция (х) е равна на или е (- 3) или е (а / 2) и уравнението

Тя има уникално решение, ако и само ако, когато

Ние решаваме уравнението графично. Построява функции

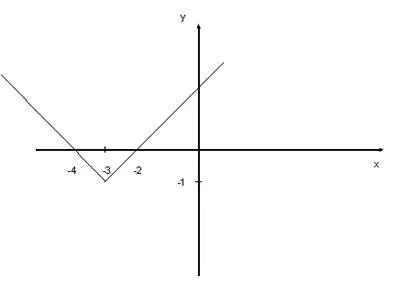
Графика функции ще бъдат конструирани така, че има една точка на пресичане на графиките. Това е възможно в два случая:

От това следва, че / 2 = - 4 или / 2 = - 2, която е = - 8, или = - 4

Помислете за всички модули за оповестяване случаи и да се покаже на пространственото решение на уравнението на координатната равнина АОХ на.

Уравнението има уникален разтвор на точките А = - 4 и а = - 8. Тези стойности са открити чрез нанасяне на линейна функция, или от съответните уравнения.

Резултатът от студента по темата е представена

Предизвикателства за определяне на стойностите на полето на функцията

V4.Naydite-малката стойност на функцията

Пишем функция под формата

Домейнът на функцията: sin3x + 5 0 sin3x -5

Важи за всяко х.

Тъй като функцията на въпросната е периодична с период, а след това считаме, че поведението на функцията и нейната производна на интервала

Функция отнема най-малката стойност на мястото.

Пишем функция под формата

Домейнът на функцията: sin3x + 5 0 sin3x -5

Важи за всяко х.

Функция увеличение на [4, 6], следователно, се най-малката стойност в точка 4.

В един от тези сесии чирак бе представен със селекция от абстрактен и решаване на проблеми по този въпрос.

Организиране на такава работа, учител "убие" няколко заека с един куршум носи колективната повторение, по-задълбочено обучение на студентите силна и нарастваща колекция от дидактически материали.