Научете как правилно да се говори Nagibin 1984 е

Научете как правилно да се говори

"След това, в началото на учебната година, трябваше да чуете разговор между две момичета на старшият от тях се премества в шести клас, най-младият - на пето момичета споделиха своите впечатления за уроци, учители, приятели, нови теми, грейдер много изненадан геометрия урок ..:. "Това е чудеса - каза тя. - учител влезе в клас, съставен от две еднакви триъгълници борда, а след това урок ни доказва, че те са равни. Не мога да разбера защо е необходимо И как смяташ да се отговори, "-., каза по-младото момиче" Научете от книгата ?.? "." това е просто много трудно да си спомните къде какво писмо да достави. "Така започва историята на интересна книга А. И. Fetisova" На доказателството в геометрията "(1954 г.).

Н. К. Krupskaya (1869-1939). "Когато децата да разберат връзката на математиката с други клонове на знанието, математика оживяват, ще омайвам от трудната предмета ще се превърне в клон на знанието"

Аз също много пъти чух от шести клас, те не разбират защо трябва да се докаже, аргументи геометрични теореми. "Това, което вертикалните ъгли са равни - те казаха - това е толкова ясно." "Какво е равностранен триъгълник, базовите ъгли са равни - това представлява схема, което е там друга причина.?" - те се чудеха. Беше невъзможно да се оставят такива въпроси без отговор, както и че е трябвало да говори с учениците за математически доказателства. На един от тези разговори, казвам ви.

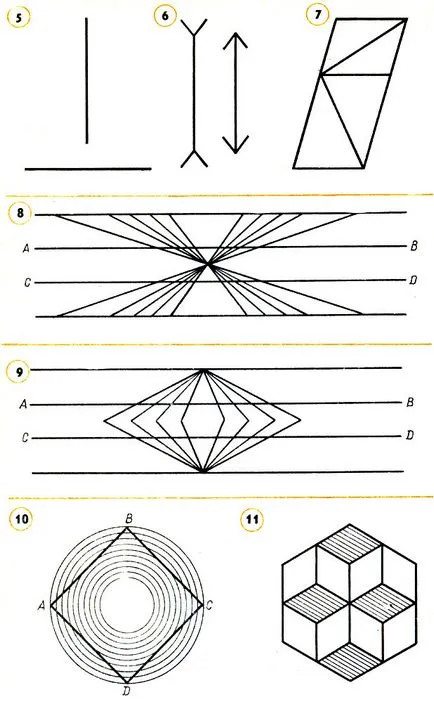
Фиг. 5. Фиг. 6. Фиг. 7. Фиг. 8. Фиг. 9. Фиг. 10. Фиг. 11

Шестокласничката Борис ми каза, че геометричните теореми за доказване на рисунки. "Вижте чертежа, и веднага се вижда, че теоремата е вярно око не заблуждава." - каза той. Имам под ръка този път се оказа, някои интересни цифри, а аз ги показа на Бор. "Сравняване на дължината на двата сегмента тук" - попитах (Фигура 5.). Борис погледна чертежа и се усмихна и каза: "Разбира се, вертикалната дължина". "А сега?" - и аз показа второ теглене (Фиг.6.). "Левицата е по-дълго" - каза Борис. "Но двете Parallelograms (фиг. 7), и всеки един от тях, проведени диагонал. Сравнете ги." И този път, заяви уверено, че по-ниската диагонала вече Борис. Тогава аз предложих Борс владетел за измерване на всички сравняват сегменти. Той доброволно се ангажира това, аз не се съмнявам, че измерванията само потвърждават своите отговори. Въпреки това, измервания са показали, че във всяка от тези фигури сравняваните сегменти на дължина, равна. Борис не го вярвам и отново започна да се измери. Новите измервания са го довели до същия извод. Бори лицето изрази объркване. Той примигна, опитвайки се да разбера какво става.

После показа Борс три рисуване (Фигура 8, 9, 10 ,.) и поиска да се инсталира - прави или криви линии AB и CD в тези цифри? Отговорът беше: "Разбира се, криви." Отново Борис объркани, когато е прикрепен към тези линии варират и е установено, че всички линии са прави.

И накрая, аз показа Борс друг чертеж (фиг. 11) и попита какво е изобразено на нея. Той погледна и каза: "Има са показани три зара:. Един в горната част и две в долната част" "Виж отново, - казах аз - така ми се струва, че горната част на двата зара, и един за тях." Борис погледна отново. "И това е вярно, две в горната част и един в долната част. Защо съм първоначално мислех обратното? Чакай, да се изправя, отново две в долната част и един в горната част." Борис разтърка очи в изненада. "Как така? Отново, две на върха и един в долната част. Странно".

След всички тези демонстрации ми остана да попитам Boria: "Възможно ли е да се докаже теоремата чертежи ли очите ни могат да ни заблудят" И Борис откровено призна, че разглеждането на чертежи може да доведе до погрешни заключения, а след това се замисли за момент и оживяване, заяви: ". На око не може да се има доверие и трябва да се измери" Аз трябваше да продължи разговора. Казах Борс, че всяко неточно измерване, освен изпълняват своите често е трудно. Може, например, да не бъде под ръцете на правилните инструменти. Но най-важното - в другата. Можете да измерите един или повече сегменти, един или повече ъгли, и така нататък. На. Но всички парчета формират под внимание, не може да се измери. И това, което е вярно за всеки два триъгълника, измерени не може да бъде валидно за другите два триъгълници. Как е възможно това? Изводът се прави Борха. "Няма за какво да се направи, ще трябва да се научи да говори, да се докаже, теореми." Това беше един добър завършек. В действителност, ние трябва да се научим да се коригира логическо мислене.

В края на разговора, който каза, Бор, че наскоро чух и гледах на урок геометрия в 6-ти клас. В този урок, преди да научат на теоремата за свойствата на равнобедрен триъгълник експериментална работа е извършена. Всеки студент в своята тетрадка привлече равнобедрен триъгълник с транспортир и измерване на ъгли в основата на триъгълника. След това се стигна до заключението, че, вероятно, базовите ъгли на равнобедрен триъгълник са равни. Формулиран е теорема, а след това учителят каза: "Ние сме тествали теорията на ъглите в основата на равнобедрен триъгълник 35 такива триъгълници (в клас е 35 студенти), а за тях това теоремата е вярна това веднага да се направи заключение, че това ще се отнася и за всеки друг. равнобедрен триъгълник? или може би, за тридесет и шести триъгълника черпим, той ще бъде наред? Как може да бъде това? притекат на помощ на разсъждение, а след няколко минути ние ще направим това, което не може да се направи с помощта на експериментална проверка, ако продажбите Този тест участват всички ученици във всички училища. С помощта на логически разсъждения, ние доказваме тази теорема за всички видове равнобедрен триъгълници. Това е най-важната роля на разсъждение "в геометрията. След урока е проведено доказателство за това теорема.

Обясних Бор, че доказателството за всяка теорема - верига от логически удръжки, които намаляват този теорема към вече доказани теореми и аксиоми и определения, въведени. Но преди това доказана теорема намалява до теорема, които са доказали, че преди. В крайна сметка, всички теореми са въз основа на приетите аксиоми.

Доказателствата за теореми са постоянно използват математически понятия. Повечето математически понятия са дефинирани. При определяне на нова концепция използват други понятия, които трябва да бъдат вече са известни. Но това намаляване на някои понятия, за другите не може да бъде безкраен. Трябва да са оригинални концепции, първична неделими до другия, неоткриваеми. Примери за това са понятията: задайте точка номер, разстояние и др. Те могат да се обяснят, описване, даде конкретни примери, но не е определена. Всички тези ученици трябва да се научат добре, а след това много трудност обучение по математика, ще бъдат преодолени.

Борис слушаше много внимателно към мен. И когато ние се разделихме, той каза, че разбира защо е необходимо да се докаже теоремата, както това е направено в класната стая.

Има една наука, тя се нарича логика, която учи как да говори с нашето мислене е определено, съгласувана, последователна, убедителни и последователни. Като човек, който не знае правилата на аритметиката и граматика, не могат да четат и пишат правилно компетентно, и хора, които не знаят правилата на логиката, не е съдържащи грешки говори и действа. Така че, на съветския народ, за да донесе повече полза нашата велика родина, причината за изграждането на комунизма, трябва да притежава логика.

Човече, да смята, често е необходимо да се дефинира понятието, за да разберете връзката между тях, помислете за това, което групата (видове) могат да бъдат разделени форми, цифри, функционални уравнения и т. D. Но много често в математика сметки от мотивите да се изведе най-различни формули, правила и доказват теореми. Не случайно са били такива, математици, които мислеха, че математиката - ". За производството на необходимите заключения" наука Такова едностранно оглед на математиката, но е вярно, че няма логика не може да бъде математиката. Това означава, че за успешното изучаване на математика, ние спешно трябва да се научим да се разсъждава правилно. Това също така означава, че много изучаване на математика е много полезно за изучаване на правилата и законите на мисълта. Не без причина понякога се нарича математика "пробен камък за ума." Не е случайно, MI Калинин каза учениците от средните училища в квартала Ленинский на Москва, че "математика дисциплини на ума, учи логическо мислене Нищо чудно, те казват, че по математика -... Той умствени гимнастика аз не се съмнявам, че имате главата нахлува с идеи но тези идеи трябва да се организират, дисциплина, напред, така да се каже, в посока на полезна работа. това е математика и да ви помогне да се справят с тази задача. "

Живот, по-специално оборудване, както и много на науката и математиката всички поставят нови предизвикателства. Математиците трябва да разработи математически въпроси теория и създаване на методи, които предоставят решения, възникнали в различни науки и проблеми практики. Как да въведете математика? Решението на всички проблеми в математиката - е преди всичко една верига от разсъждения. Изчислената, конвертиране, изграждане на които толкова често, че трябва да се използва за решаване на проблемите, които е невъзможно без логическо мислене: доводите си, които са изпратени. Така че, по математика не може без логика.

М. И. Калинин (1875-1946) "Всички студенти трябва да имат предвид, че само един човек ще има някакво значение в обществения живот, в който и да е от полза на кариерата, който знае как да работи систематично с познания по случая"

Математика също помогна за откриването на много малки планети като Серес. Ceres се наблюдава за първи път от астроном Piazzi, но поради прекъсване на наблюденията го е загубил. Той дойде на помощ на известния математик KF Гаус. С някои данни за новата планета, получен чрез Piazzi, той изчислява своята орбита. В действителност, според указанията на Гаус, Ceres е преоткрит.

Ето още един пример, който илюстрира стойността на логика в областта на математиката. В древни времена хората са се опитвали да намерят емпирично отношението на дължината на окръжността към нейния диаметър, т.е. Ние се опитваме да намерим число, което показва колко по-дълго от обиколката на нейния диаметър. Този номер, означена с буквата П (PI) *. ние трябва да се използва при изчисляване на известни дължината на диаметъра на окръжността и площта на кръг, както и за много други важни задачи.

* (Това название използвано за първи път през 1706, на английски математик Уилям Джоунс, и то е станало обичайно за 1736, когато той започна систематично Яжте Ойлер.)

Така че, това е необходимо, за да се изчисли с точност стойността на π. Експериментална изчисление може да даде само доста приблизително резултата. В ранните етапи на човешката култура използва тези неточни стойности л. В древен Египет, например, преди повече от 3000 години е смятан за номер П равно на 3. В III. Преди новата ера. д. един от най-големите математици на древна Гърция, талантлив изобретател, истински син на родината си, починал от враговете й, Архимед без измерване, единствено от съображения и изчисления намерени резултати за броя на литра сравнително точна стойност 3 1/7 (Archimedean номер). По-късно други математици, като се използват за откриването на Архимед, изчислени π с още по-голяма точност. Така че, в XVI век. Немски математик Ludolph, като е прекарал много време, изчислен 35-те знака след десетичната цифри на този номер. Ludolfovo стойност на π е: 3,14159265358979323846264338327950288. Изчисляване на по-точни стойности L след Ludolfs въз основа на други съображения, не са спрели. През 1873 математик Шанкс изчисляват 527 знака след десетичната запетая на числото. Шанкс, обаче, изчислява общата сума на 707 знака след десетичната запетая, но като се започне с 528-секунди, неговите признаци са грешни. Тази приблизителна стойност на пи, което е намерено Шанкс вероятно няма практическо значение. И все пак, изчисляването на нови признаци на продължи л. През 1946-1947. в Англия и Съединените щати с помощта на компютър, изчислена 808 знака след десетичната запетая на числото през 1949 - 2035 знака, а след 3089 знака. В момента има повече от 10,000 цифри от L, както и изчисляването на нови герои носи някои практически предимства: например за обработка на проверка мощност на съвременните компютри и софтуер за тях. Виждаме, че логическото разсъждение, ще даде възможност за развитие на геометрията и други части на математиката, предоставя възможност за изчисляване на броя на литрите и много други често използвани номера (константи) с някаква степен на точност, без каквато и измерване.

Всички по-горе води до заключението за необходимостта от постоянна учене да се разсъждава логично. Всеки студент трябва да уча трудно да се мисли правилно.

Може би това трябва да се прави само в гимназията? Научете се да причина логично се нуждаят от много и постоянно във всички училищни степени.